Lineare Funktionen: Schnittpunkte mit Achsen, Steigungswert und Steigungswinkel berechnen

Question

Berechnen Sie die Schnittpunkte der Graphen von f mit den Koordinatenachsen und zeichen Sie den Graphen. Wie groß sind der Steigungswert und der Steigungswinkel?

a) f(x) = 1 - x

b) f(x) = 0.5 x - 2

Answer 1

Grundsätzliches Wissen gibt es im Video "Lineare Funktionen (Einführung)":

Lektion: https://www.matheretter.de/wiki/lineare-funktionen

Der Wert vor dem x gibt dir also die Steigung an.

a) f(x) = 1 - x
kannst du umstellen zu: f(x) = - x + 1
und das -x kannst du schreiben als: f(x) = -1*x + 1
-1 ist die Steigung (nach unten)

b) f(x) = 0.5 x - 2
0.5 ist die Steigung (nach oben)

Mit dem Funktionsplotter kannst du dir selbst die Funktionen einzeichnen:

f(x) = -1 x + 1
g(x) = 0.5 x - 2

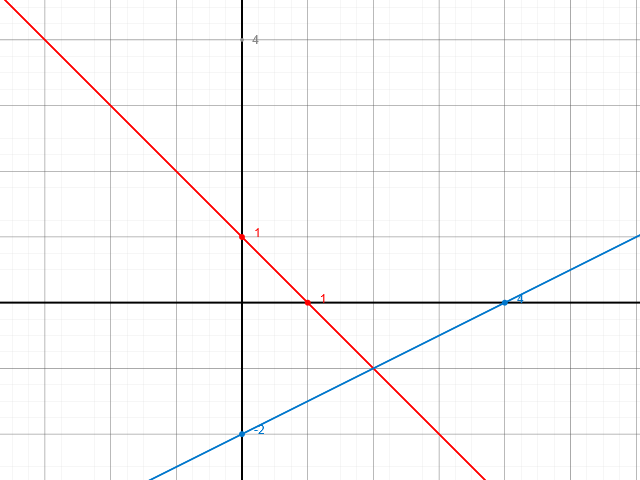
Schnittpunkt mit y-Achse erkennst du am absoluten Glied der Funktionsgleichung bzw. du setzt für x=0 ein:

f(x) = -1*x + 1 = y
f(0) = -1*0 + 1 = 1  →  P(0|1)

g(x) = 0.5*x - 2 = y
g(0) = 0.5*0 - 2 = -2  →  P(0|-2)

Schnittpunkt mit x-Achse (Nullstelle) erhältst du, indem du die Funktionsgleichung Null setzt und umstellst:

f(x) = -1*x + 1 = y
-1*x + 1 = 0    | -1
-1*x = -1   | :(-1)
x = 1

g(x) = 0.5*x - 2 = y
0.5*x - 2 = 0   | +2
0.5*x = 2  | :0.5
x = 4

Steigungswinkel erhält man zum Beispiel über den Arkustangens aus der Steigung:

f → tan^-1(-1) = -45°
g → tan^-1(0.5) ≈ 26,565°

Answer 2

a) f(x) = 1 - x

y-Achsenabschnitt f(0)
f(0) = 1

Nullstelle f(x) = 0
1 - x = 0
x = 1

Steigung ist der Koeffizient vor dem x: m = -1

Steigungswinkel = arctan(-1) = -45 Grad

 

b) f(x) = 0.5 x - 2

y-Achsenabschnitt f(0)

f(0) = -2

Nullstelle f(x) = 0
0,5x - 2 = 0
x = 4

Steigung ist der Koeffizient vor dem x: m = 0,5

Steigungswinkel = arctan(0,5) = 26,57 Grad