f(x)=x^3 −3x^2+3x
f(x)=0
x^3 −3x^2+3x=0
x*(x^2-3x+3)=0
x₁=0 x₂ und x₃ liegen in ℂ
f´(x)=3x^2-6x+3
Nullstellen von f´(x)
3x^2-6x+3=0
x^2-2x=-1
(x-1)^2=-1+1=0| \( \sqrt{} \)
x₁ und x₂ =1 → doppelte Nullstelle
Monotonie kann sich nur an Nullstellen der ersten Ableitung ändern:
f´(0) =3*0-6*0+3=3 3 ist nun größer als 0 Somit ist f monoton steigend im Intervall (-∞,1]
f´(2) =3*2^2-6*2+3= 3 ist nun größer als 0 Somit ist f monoton steigend im Intervall [1,∞)
Somit ist f(x)=x^3 −3x^2+3x im gesamten Bereich (-∞,∞)
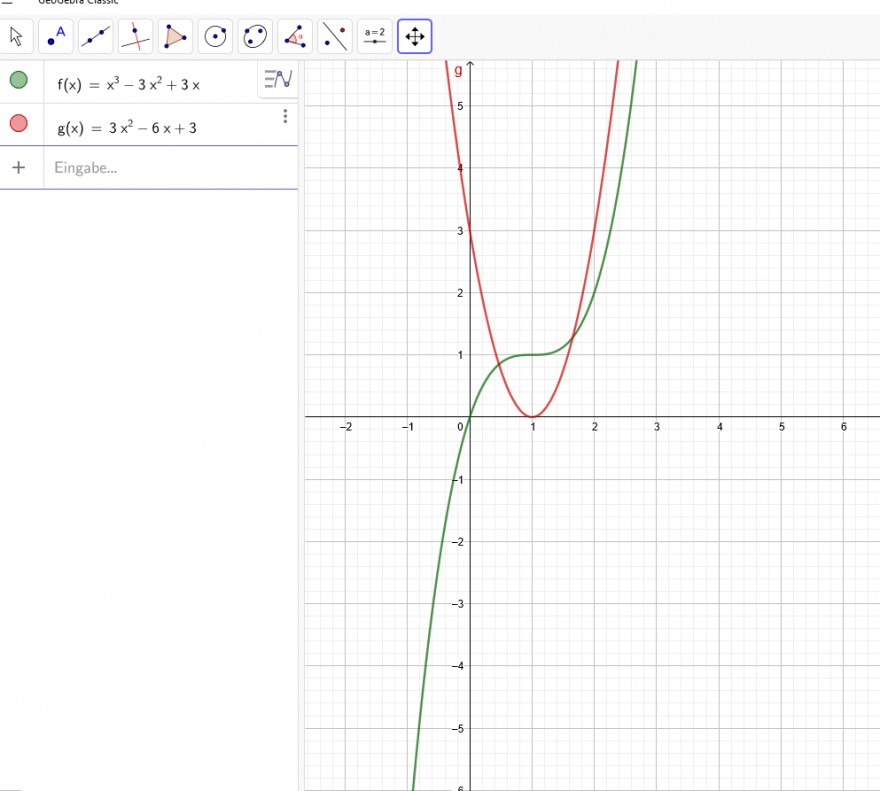
Text erkannt:
\( f(x)=x^{3}-3 x^{2}+3 x \)
\( f(x)=3 x^{2}-6 x+3 \)
\( +\quad \) Eingabe...