Hallo,
eine Skizze ist immer wichtig! (Maße in \(\text{cm}\))
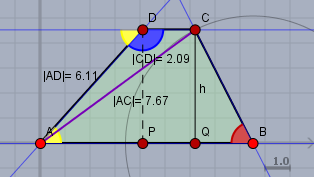
berechne zunächst die Höhe \(h\) des Trapez. Im Dreieck \(\triangle BCQ\) gilt$$\sin(\beta) = \frac{h}{|BC|}$$und daraus folgt$$h = |BC| \sin(\beta) = 51\,\text{mm} \cdot \sin(63°) \approx 45,4\,\text{mm}$$Im Dreieck \(\triangle APD\) gilt$$\sin(\alpha) = \frac{h}{|AD|}$$und \(\alpha\) (gelb) ist der Nebenwinkel von \(\delta\) (blau). Folglich ist \(\alpha = 180°-\delta\), aber da allgemein gilt \(\sin(x) = \sin(180°-x)\), ist auch$$\sin(\delta) = \frac{h}{|AD|} \\\implies |AD| = \frac{h}{\sin(\delta)} \approx \frac{45,4\,\text{mm}}{\sin(132°)} \approx 61,1\,\text{mm}$$Um die Seite \(|CD|\) zu berechnen, macht man sich zunutze, dass$$|CD| = |AB| - |BQ| - |AP|$$und mit$$|BQ| = |BC| \cdot \cos(\beta) \\ |AP| = |AD| \cos(\alpha) = - |AD| \cos(\delta)$$kommt man dann zu \(|CD| \approx 20,9\,\text{mm}\).
Die Länge der Diagonale \(|AC|\) liefert Pythagoras$$|AC|^2 = |AQ|^2 + h^2 \implies |AC| \approx 76,7\,\text{mm}$$