Rotation berechnen(Vase)

Question

Aufgabe:

Bei einer Vase der Höhe 40 cm beträgt der Radius oben 6 cm, in der Mitte 10 cm und
unten 8cm. Wie groß ist ihr Volumen V? Berechnen Sie das Volumen mit Hilfe der
Trapez-Regel und der Simpson-Formel.
Hinweis: Die Vase soll durch Rotation des Graphen von f um die x-Achse erzeugt
werden.

$$V = π*\int \limits_{0}^{40}f(x)^2 dx$$

Problem/Ansatz:

Könnt ihr mir bitte bei dieser Aufgabe helfen?

Vor allem, wie man die Stützwerte einsetzen muss (und dann einsetzt).

Answer 1

Sieht wohl so aus:

~draw~ polygon(-20|6 0|10 20|8 20|0 -20|0);zoom(20) ~draw~

Trapezregel : Es gibt also 2 Trapeze, die rotieren um die

x-Achse und erzeugen dabei Kegelstümpfe.

Der erste hat die Radien r1=6cm und r2=10cm und die Höhe h=20cm

also Volumen V=pi*h/3 *(r1² + r1r2 + r2²)

                   = pi*20/3 *(36 + 60 + 100) cm³

                  ≈4105 cm³.

So ähnlich bestimmst du auch den 2. Kegelstumpf.

Answer 2

Ich habe eine Zeichnung mit den Stützstellen angefertigt. Zur Aufstellung von f(x) würde ich in den Stützstellen waagerechte Tangenten vorschlagen.

Trapez-Regel und der Simpson-Formel sind mir nicht geläufig.

Answer 3

Hallo,

Sowohl die Trapez-Regel als auch die Simpson-Formel ermitteln näherungsweise den Wert eines Integrals. Hier sind drei Stützstellen gegeben:$$f(0)^2 = 8^2 = 64 \\ f(20)^2 = 10^2 = 100 \\ f(40)^2 = 6^2 = 36$$Bei drei Stützstellen hat man zwei Segmente und nach der Trapezregel ist$$\begin{aligned}\int_0^{40} f(x)^2\,\text dx &\approx \frac {20}2(64+100) + \frac{20}2(100+36) \\&= 1640+ 1360 = 3000\end{aligned}$$und wenn man die gleichen drei Werte in die Simpson-Formel einsetzt, erhält man$$\begin{aligned}\int_0^{40} f(x)^2\,\text dx &\approx \frac{40}{6}(64 + 4\cdot 100 + 36) \\&= \frac{20000}6 \approx 3333\end{aligned}$$Multipliziert mit $\pi$ gibt das einmal ein Volumen von $V_T \approx 9,42 \,\text l$ und einmal $V_S\approx 10,47\,\text l$.

Hier noch mal ein Vergleich der beiden Graphen der Näherung von $f(x)^2$, die von Trapez- (blau) und Simson-Formel (rot) berechnet werden.
Plotlux öffnen

Zoom: x(-5…45) y(-5…105)f₁(x) = (9x/5+64)·(x>0)·(x<20)+(-16(x-20)/5+100)·(x>20)·(x<40)f₂(x) = -x²/8+4,3x+64

Das Integral ist dann jeweils die Fläche unter der Kurve im Intervall $x=0$ bis $x=40$.

Welches Ergebnis davon nun näher an der Wahrheit liegt, lässt sich nur beantworten, wenn man weiß wie die Vase wirklich aussieht. Besteht sie aus zwei zusammengesetzten Kegelstümpfen - so wie hier

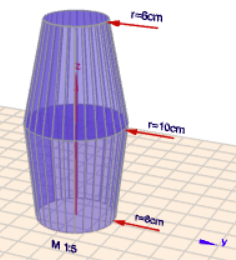
oder ist sie eher bauchiger Natur

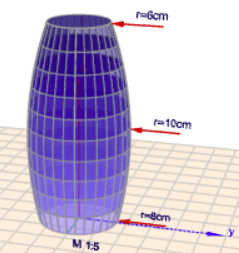
Die untere Vase hat natürlich ein etwas größeres Volumen.

Beide Volumina lassen sich auch exakt berechnen. Wobei das Profil der bauchige Vase durch eine Parabel approximiert wurde. Das führt dann zu folgenden Graphen von $f(x)^2$

Plotlux öffnen

f₁(x) = (64+8x/5+x²/100)·(x>0)·(x<20)+(196-28x/5+x²/25)·(x>20)·(x<40)Zoom: x(-5…45) y(-5…105)f₂(x) = ((((9x/160000-3/800)·x-23/400)·x+4)·x+64)

Wohlgemerkt(!) es ist der Verlauf von $f(x)^2$ und nicht das jeweilige Profil der Vase. Die Stücke des blauen Graphen sind Parabeln und die rote Kurve ist vom Grad 4.

Die keglige Vase hat ein Volumen von $V_k \approx 9,22\,\text l$ und die bauchige von $V_b \approx 10,32\,\text l$, was wiederum nur wenig unterhalb der Näherungslösung liegt.

Gruß Werner