Hallo,
Deine Frage deutet darauf hin, dass Du Dir noch keine Zeichnung gemacht hast - oder? Klar, es ist nicht einfach, sich das in 3D aufzumalen, aber man kann sich auch auf 2 Dimensionen (hier z.B. y und z) beschränken. Das ändert vom Prinzip her rein gar nichts.
Also zeichne Dir mal die Gerade, so wie oben angegeben, mit ihren Y- und Z-Koordinaten auf:$$g: \quad \vec x = \begin{pmatrix}{\color{grey}1}\\ 1\\ 2\end{pmatrix} + t \cdot \begin{pmatrix}{\color{grey}0}\\ -2\\ 7\end{pmatrix}$$
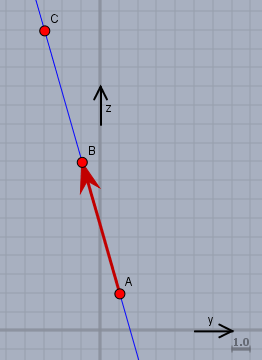
Dort siehst Du die Gerade (blau) und den Punkt \(A(y=1|\, z=2)\) sowie den roten Richtungsvektor \(\vec r\), der in Richtung \((y=-2|\, z=7)\) zeigt.
a) Geben Sie drei Punkte an, die auf der Geraden g: x= (1/1/2)+t • (0/-2/7) liegen.
Man erhält beliebige Punkte auf der Geraden indem für den Parameter \(t\) eine beliebige Zahl einsetzt. Also z.B. \(t=2\) $$\vec x(t=2) = \begin{pmatrix}1 \\ 1\\ 2\end{pmatrix} + 2 \cdot \begin{pmatrix}0\\-2\\ 7\end{pmatrix} = \begin{pmatrix}1\\-3\\ 16\end{pmatrix} =C$$Genauso erhält man den Punkt \(A\) für \(t=0\) und den Punkt \(B\) für \(t=1\) (s. Skizze).
b) Geben sie eine weitere Gleichung der Geraden g an.
Sei eine Geradengleichung in Parameterform gegeben$$g: \quad \vec x = A + t \cdot \vec r, \quad \text{hier:}\space A= \begin{pmatrix}1 \\ 1\\ 2\end{pmatrix}, \quad \vec r = \begin{pmatrix}0\\-2\\ 7\end{pmatrix}$$Dann ist jede Gerade \(g'\) in Parameterform deren Aufpunkt auf \(g\) liegt und deren Richtungsvektor \(\vec r'\) ein Vielfaches von \(\vec r\) ist, identisch zu \(g\).
Beispiel: der Punkt \(B\) $$B = \begin{pmatrix}1\\-1\\ 9\end{pmatrix} = \vec g(t=1)$$liegt auf \(g\) und der Vektor \(\vec r'\) $$\vec r' = \begin{pmatrix}0\\4\\ -14\end{pmatrix} = (-2) \cdot \vec r$$verläuft parallel zu \(\vec r\), dann ist $$g': \quad \vec x = B + s \cdot \vec r' = \begin{pmatrix}1\\-1\\ 9\end{pmatrix} + s \cdot \begin{pmatrix}0\\4\\ -14\end{pmatrix} \\ \implies g' = g$$die Geraden sind identisch und \(g'\) ist lediglich eine andere Darstellung von \(g\) in Parameterform.