Zeige: CE und BD sind gleichlang.

Question

Seien ABC und ADE zwei gleichseitige Dreiecke mit dem gemeinsamen Punkt A. Zeige: CE und BD sind gleichlang.

Comments

und AB senkrecht auf AE geht auch ohne

Answer 1

Die Dreiecke AEC und ADB sind kongruent:

S Seite von ABC

W Winkel bei A

S Seite von ADE

:-)

Answer 2

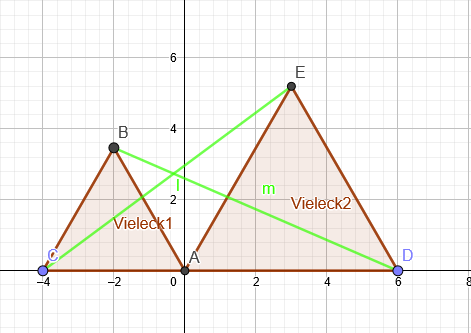
Koordinaten von C :  C(-4|0)

Koordinaten von B: Kreis um A(0|0)  mit r=4   :           1.)  x^2+y^2=16

und Kreis um C C(-4|0)  mit r=4:   (x+4)^2+y^2=16 → 2.) x^2+8x+y^2=0

2.)-1.)  8x=-16   → x=-2  in 1.) 4+y^2=16  → y₁=2\( \sqrt{3} \)       y₂=-2\( \sqrt{3} \)

B₁(-2|2\( \sqrt{3} \))  und B₂(-2|-2\( \sqrt{3} \))

Gleiches Vorgehen bei den Punkten E und D:

D(6|0)       E₁(3|3\( \sqrt{3} \)) und E₂(3|-3\( \sqrt{3} \))

Kreis um B₁(-2|2\( \sqrt{3} \)) :

(x+2)^2+(y-2\( \sqrt{3} \))^2=r₁^2

D(6|0)

(6+2)^2+(0-2\( \sqrt{3} \))^2=r₁^2

64+12=r₁^2        r₁=\( \sqrt{76} \) 

Kreis um E₁(3|3\( \sqrt{3} \))

(x-3)^2+(y-3\( \sqrt{3} \))^2=r₂^2

C(-4|0)

(-4-3)^2+(0-3\( \sqrt{3} \))^2=r₂^2

49+27=r₂^2       r₂=\( \sqrt{76} \)

r₁=r₂    →   q.e.d.