Rotationskörper berechnen mittels Integration

Question

Ich komme gerade nicht so gut mit der Mathe Aufgabe klar. Weiß einer wie ich vorgehen müsste?

Vielen Dank schonmal im Voraus :))

Text erkannt:

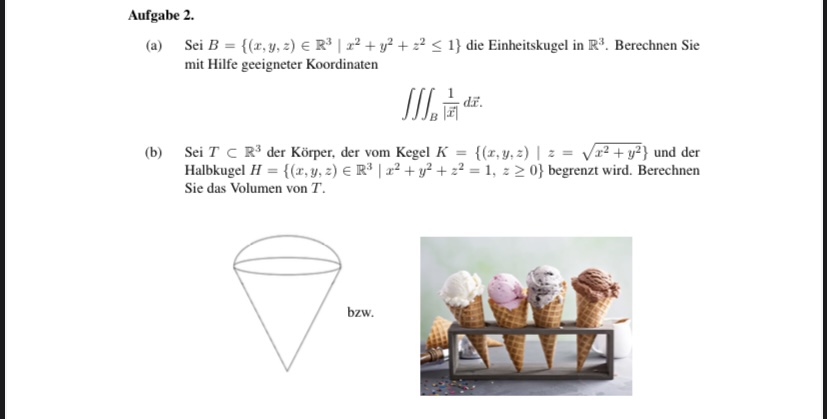
Aufgabe 2,
(a) Sei $B=\left\{(x, y, z) \in \mathbb{R}^{3} \mid x^{2}+y^{2}+z^{2} \leq 1\right\}$ die Einheitskugel in $\mathbb{R}^{3} .$ Berechnen Sie mit Hilfe geeigneter Koordinaten
$\iiint_{B} \frac{1}{|\vec{x}|} d \vec{x} .$
(b) Sei $T \subset \mathbb{R}^{3}$ der Körper, der vom Kegel $K=\left\{(x, y, z) \mid z=\sqrt{x^{2}+y^{2}}\right\}$ und der Halbkugel $H=\left\{(x, y, z) \in \mathbb{R}^{3} \mid x^{2}+y^{2}+z^{2}=1, z \geq 0\right\}$ begrenzt wird. Berechnen Sie das Volumen von $T$.

Answer 1

Hallo

 1. da es sich um eine Kugel handelt benutzt man Kugelkoordinaten, dann ist das Integral sehr leicht

2. zuerst über den Kegel, dann über den Kugelabschnitt integrieren. hier bieten sch Zylinderkoordinaten an. Zuerst natürlich die Schnittfläche bestimmen.

Gruß lul

Comments

Danke dir :)