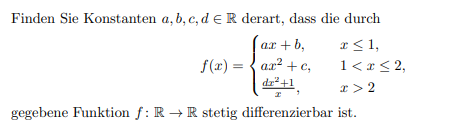
Text erkannt:
Finden Sie Konstanten \( a, b, c, d \in \mathbb{R} \) derart, dass die durch
$$ f(x)=\left\{\begin{array}{ll} a x+b, & x \leq 1 \\ a x^{2}+c, & 1<x \leq 2 \\ \frac{d x^{2}+1}{x}, & x>2 \end{array}\right. $$
gegebene Funktion \( f: \mathbb{R} \rightarrow \mathbb{R} \) stetig differenzierbar ist.