erstmal zu deinem Beispiel. Die Matrix
\( \begin{pmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} \)
ist eine Drehmatrix. Denn sie ist orthogonal \( ((P^TAP) (P^TAP)^T = E_3) \) und die Determinante ist gleich 1 \( (\det(P^TAP) = 1) \).
Die allgemeinen Formen einer Drehmatrix sind:
Drehung um x-Achse:\( \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta \\ 0 & \sin \theta & \cos \theta \end{pmatrix} \)
Drehung um y-Achse: \( \begin{pmatrix} \cos \theta & 0 & \sin \theta \\ 0 & 1 & 0 \\ -\sin \theta & 0 & \cos \theta \end{pmatrix} \)
Drehung um z-Achse: \( \begin{pmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \)
Was in deinem Beispiel nun gemacht wurde, ist, die Matrix \( P^TAP \) gleich der z-Drehmatrix zu setzen und einen Koeffizientenvergleich zu machen:
\( \begin{pmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} \) = \( \begin{pmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \)
Im 1-1-Eintrag sowie im 2-2-Eintrag sehen wir, dass \( \cos \theta = 0 \) gelten muss. Im 1-2-Eintrag muss \( -\sin \theta = 1 \) und im 2-1-Eintrag muss \( \sin \theta = -1 \) sein. Der Rest passt.
Diese Bedingungen schreiben wir nun einmal ordentlich als LGS auf,
(GL.1) \(\ \cos \theta = 0 \)
(GL.2) \(\ -\sin \theta = 1 \)
(GL.3) \(\ \sin \theta = -1 \)
wobei sofort auffällt, dass (GL.2) und (GL.3) sich nur um das Vorzeichen unterscheiden. Wir können also ohne Probleme nur
(GL.1') \(\ \cos \theta = 0 \)
(GL.2') \(\ \sin \theta = -1 \)
betrachten. Dieses Gleichungssystem gilt es nun zu lösen. Als Ergebnis bekommen wir \( \theta = \frac{3}{2}\pi \), wobei \( \frac{3}{2}\pi = 270^\circ\) gilt. Das heißt, wir haben auf der rechten Seite, bei der Gleichsetzung, eine Matrix mit einer Drehung von \( 270^\circ \) um die z-Achse. Da die beiden Matrizen gleich sind, gilt dies auch für die linke Matrix, unserer ursprünglichen Matrix. Folglich erhalten wir, dass der Drehwinkel von \( P^TAP \) gleich \( 270^\circ \) ist.
Ob man es nun immer so machen kann, kann ich dir gerade nicht sagen. Was man aber immer machen kann, ist das folgende Verfahren anzuwenden:
Der Drehwinkel \(\theta\) einer Drehmatrix D ist definiert als
\(\cos \theta = \frac{1}{2}(Spur(D) - 1)\).
Die Spur einer Matrix ist die Summe seiner Diagonaleinträge:
M = \( \begin{pmatrix} m_{1,1} & m_{1,2} & m_{1,3} \\ m_{2,1} & m_{2,2} & m_{2,3} \\ m_{3,1} & m_{3,2} & m_{3,3} \end{pmatrix} \implies Spur(M) = m_{1,1} + m_{2,2} + m_{3,3}\)
oder Allgemein für eine Matrix der Dimension d:
Spur(M) = \(\sum_{n=1}^d m_{n,n} \).
Die Formel für den Drehwinkel können wir auch schreiben als
\( \theta = \pm \arccos ( \frac{1}{2}(Spur(D) - 1) ) \),
wobei man hier aufpassen muss, dass wir hier ein \( \pm \) stehen haben. Ob der Drehwinkel nun positiv oder negativ ist, hängt von der Drehachse ab. Das ist aber gar nicht so schwer, herauszufinden, welches Vorzeichen wir haben. Die Voraussetzung dafür ist, dass wir die Drehachse kennen oder vorhin berechnet haben. Die Drehachse definiere ich mal als \( \vec{n} \). Folgende Schritte sind nun zu machen:
- Bestimme einen beliebigen Vektor \( \vec{v} \), der senkrecht auf deiner Drehachse steht.
- Multipliziere diesen Vektor nun mit deiner Drehmatrix D: \( D\vec{v} = \vec{w} \).
- Bilde das Kreuzprodukt \( \vec{v} \times \vec{w} = \vec{z}\).
Nun gilt es, die Vorzeichen von \( \vec{z} \) und \( \vec{n} \) zu vergleichen:
\(\theta = \left\{\begin{array}{cc} \arccos ( \frac{1}{2}(Spur(D) - 1) ) & \text{Vorzeichen stimmen überein} \\ -\arccos ( \frac{1}{2}(Spur(D) - 1) ) & \text{Vorzeichen sind verschieden} \end{array}\right.\).
Warum dieses Verfahren? Kennen wir die Drehachse, bestimmen wir einen Vektor, der senkrecht auf dieser Drehachse steht. Mit der Multiplikation der Drehmatrix drehen wir diesen Vektor um den, uns noch unbekannten Winkel, \( \theta \). Bilden wir nun das Kreuzprodukt von \( \vec{v} \) und \( \vec{z} \), erhalten wir einen Vektor, der senkrecht auf diesen beiden steht. Dieser ist nun aber per Konstruktion parallel zur Drehachse. Sind die Vorzeichen gleich, zeigt der Vektor \( \vec{z} \) in die gleiche Richtung.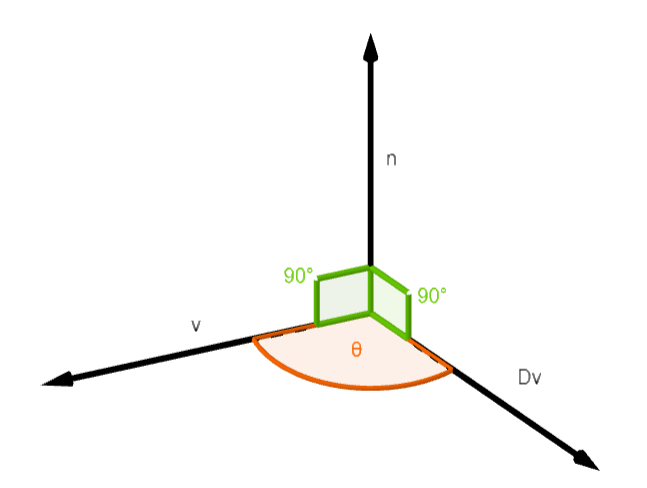
Sollte noch etwas unklar sein, frag gerne nach.
Lg
