Aufgabe:
Zu zeigen ist, dass folgende Gleichung für ein gegebenes Intervall gilt.
Text erkannt:
und surjektiv ist.
(b) Zeigen Sie, dass für jedes \( x \in[-1,1] \) die Ungleichung \( \sqrt{1+x} \leq 1+\frac{x}{2} \) gilt.
Problem/Ansatz:
Mir ist nicht klar, wie man folgendes beweisen kann.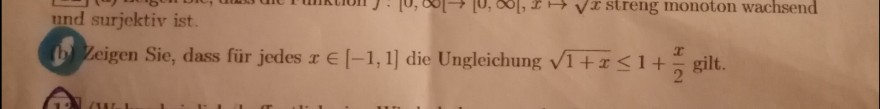
Ich habe es wie folgt versucht:
die Ungleichung habe ich nach x aufgelöst und bin auf x≥0 gekommen.
Könnte mir bitte jemand einen Tipp geben?
Danke, V.