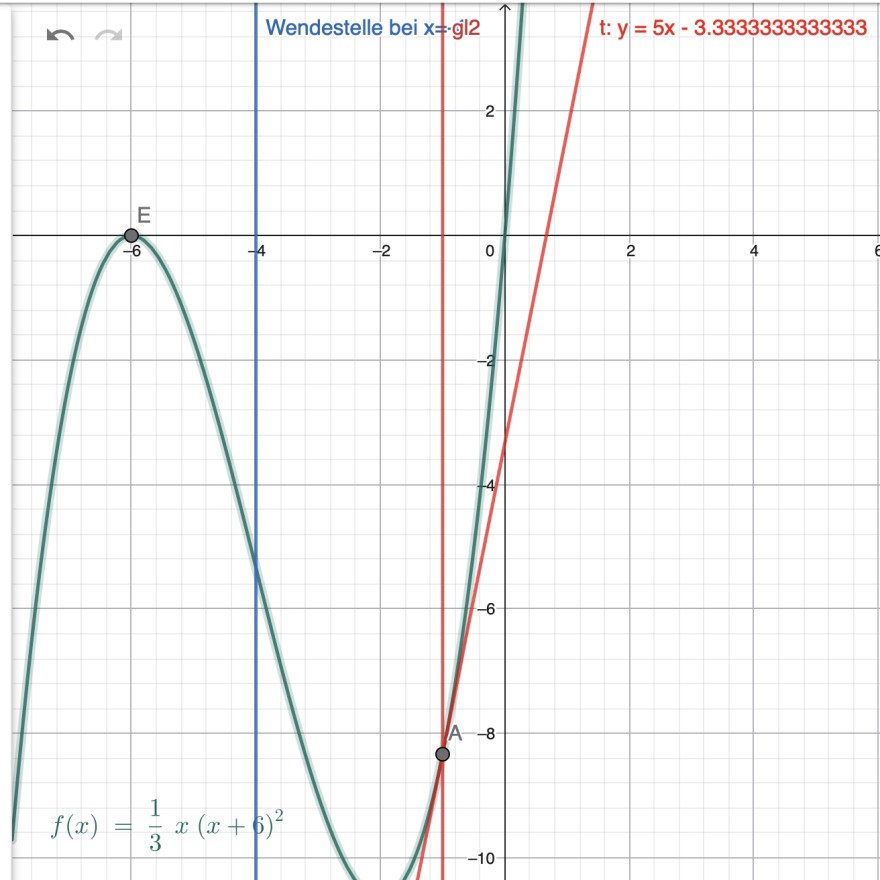
Ich suche ein Polynom 3. Grades mit folgenden Eigenschaften:
- Wendestelle bei x=-4
- Berührt die x-Achse bei x= -6
- Steigung der Tangente an der Stelle x= -1 ist 5
- Berührt die x-Achse bei x= -6: Extremstelle mit doppelter Nullstelle →. Nullstellenform:
\(f(x)=a(x+6)^2(x-N)\\=a(x^2+12x+36)(x-N)\\=a(x^3-Nx^2+12x^2 -12Nx+36x-36N)\)
- Wendestelle bei x=-4. →2.Ableitung
\(f'(x)=a(3x^2-2Nx+24x -12N+36)\).
\(f''(x)=a(6x-2N+24)\)
\(f''(-4)=a(-2N)=0\).
\(N=0\)
- Steigung der Tangente an der Stelle x=-1 ist
\(f'(x)=a(3x^2+24x +36)\).
\(f'(-1)=a(3-24+36)=15a= 5\)
\(a=\frac{1}{3}\).
\(f(x)=\frac{1}{3}(x+6)^2x \)