Benötige Koordinatensysteme für Parabeln?

Question

Grüßt euch,

Wir behandeln gerade Parabeln im Koordinatensystem. Ich habe hier 3 "Parabeln aus dem realen Leben". Dazu habe ich die Werte:

Junge, mit dem Wasserschlauch:

25cm Höhe / 40cm Breite

Tunnel, Unterführung:

3m Höhe / 2m Breite

Gebäude:

25m Höhe / 20m Breite

Könnte bitte jemand diese Parabeln sauber in ein Koordinatensystem einbringen. Damit werde ich die kommenden Wochen arbeiten müssen. (Weshalb ich es sauber brauche).

Text erkannt:

a

Comments

Vom Duplikat:

Titel: Normal und Scheitelform der Parabel?

Stichworte: parabel,scheitelform,normalform,scheitelpunktform,normale

Hallo, ich bräuchte für diese Parabel einmal die Normal und Scheitelpunktform erklärt. Dann kann ich sie auf die anderen Aufgaben anpassen.

Answer 1

Würde das wie folgt langen?

Der Junge mit dem Wasserschlauch

Für Anfänger ist es öfter einfach die Parabel Achsensymmetrisch ins Koordinatensystem zu setzen.

Comments

Hi, vielen Dank!

Könnten Sie dies für die anderen 2 Parabeln gleich tun?

Liebe Grüße,

Lisa

---

Du könntest es selber mal mit dem Programm Mathegrafix probieren.

https://www.mathegrafix.de/

---

Habe leider weder einen Laptop, noch ein anderes Gerät, auf welchem Mathegrafix funktioniert. Auch die Suche für mobile Geräte war nicht erfolgreich und auch kein "Online-Editor".

Ich wäre ihnen sehr verbunden, wenn Sie mir die anderen 2 Systeme zeichnen.

---

Tunnel

Gebäude

---

Evtl. geht auch direkt die Internetseite Geogebra oder Desmos oder ähnliche Funktionsplotter.

---

@LisaMeiland:

in folgendem Bild kannst Du die Höhe $h$ und die Breite $b$ der Parabel mit der Maus verändern.

Klicke auf das Desmos-Symbol unten rechts, so kannst Du die Werte oben links auch drekt eintragen und anschließend mit dem Maus-Rad die Größe des Bildausschnitts anpassen.

Die grüne Parabel ist die zur Y-Achse symmetrische Variante und die lilane Parabel beginnt im Ursprung.

Answer 2

Junge, mit dem Wasserschlauch:  25cm Höhe / 40cm Breite.

$f(x)=a*(x-N₁)*(x-N₂)$

$N₁(0|0) N₂(40|0)$

$f(x)=a*(x-0)*(x-40)$

$f(x)=a*x*(x-40)$

$S(20|25)$ 

$f(20)=a*20*(20-40)$

$f(20)=-400a$

$-400a=25$

$a=-\frac{1}{16}$

$f(x)=-\frac{1}{16}*x*(x-40)$

Answer 3

Vom Duplikat:

Titel: Allgemeine/Scheitelpunktform der Parabeln?

Stichworte: scheitelpunktform,parabel,funktion,allgemeinform,parabelgleichung

Hallo, ich bin es wieder!

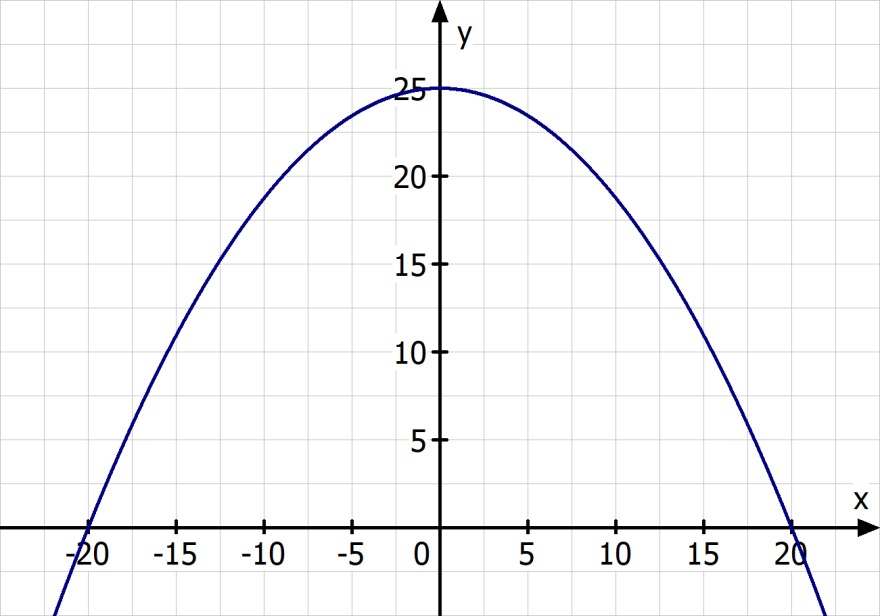
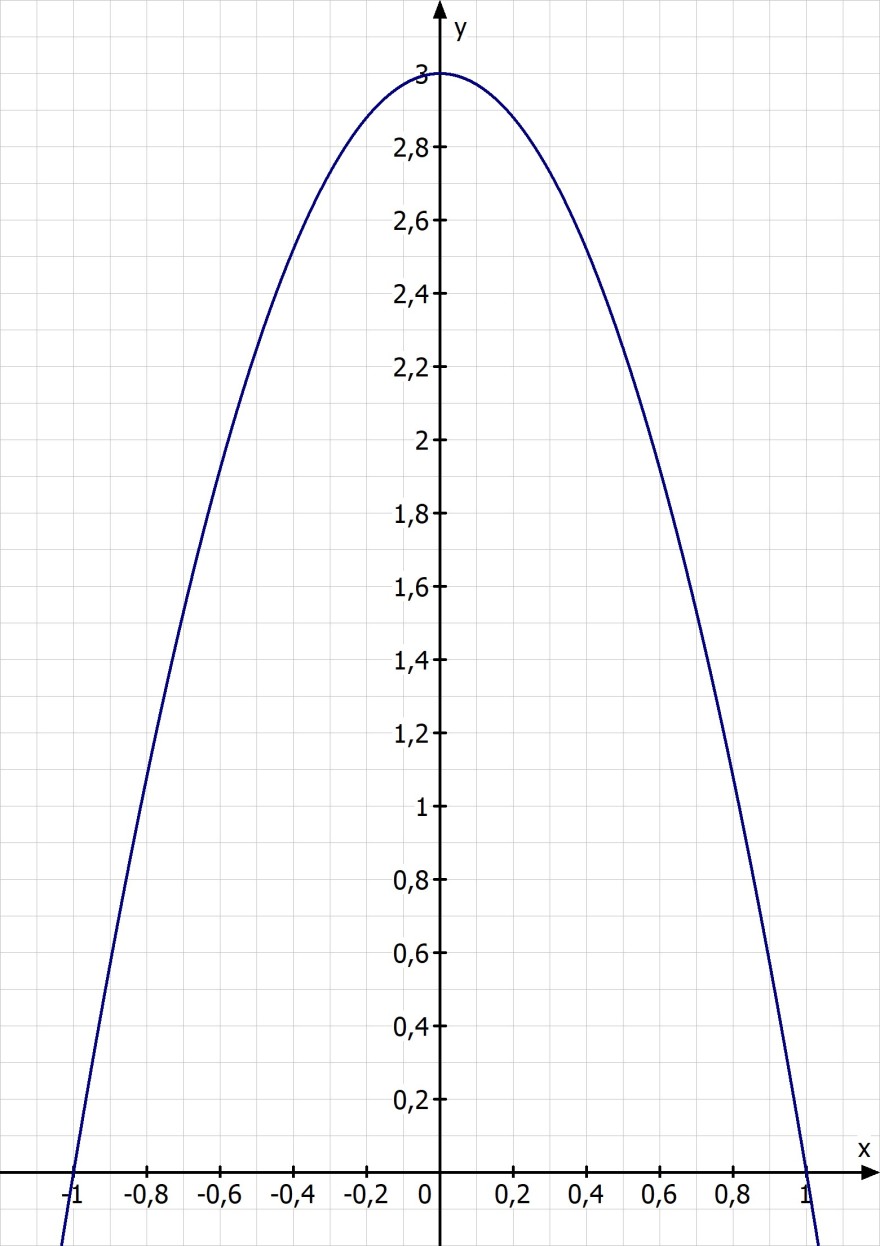
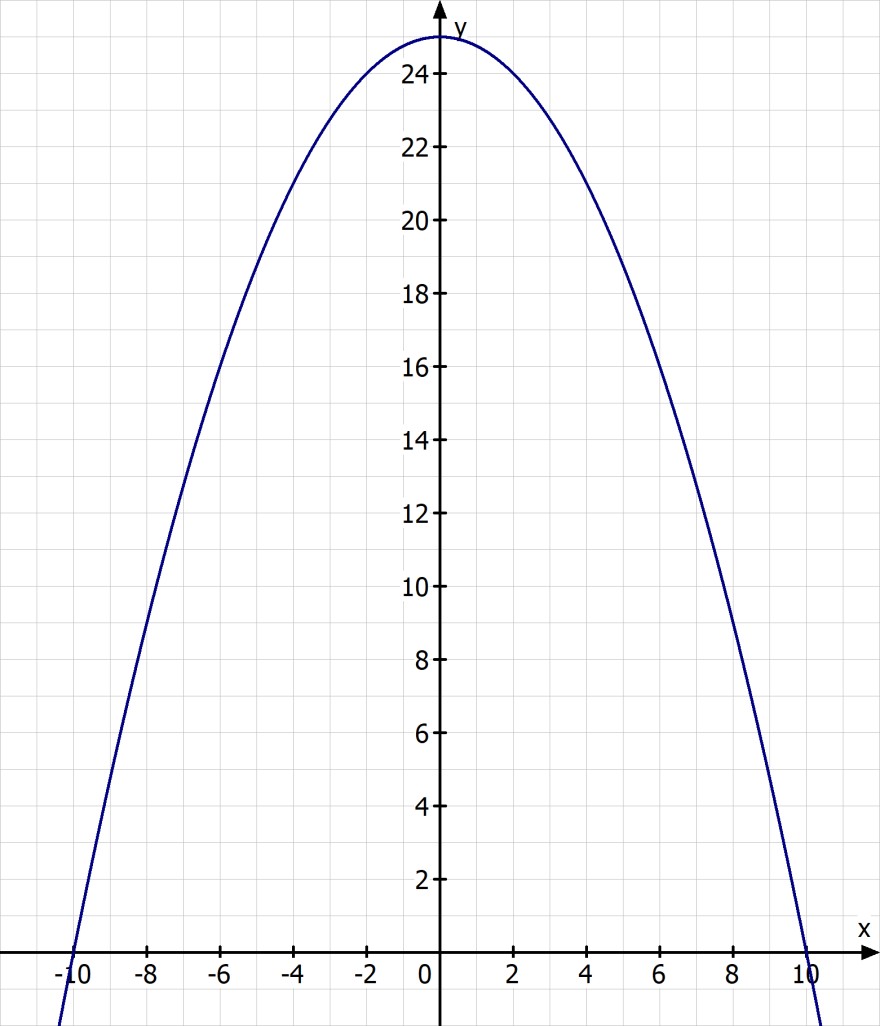
Leider fällt mir das arbeiten mit den Parabeln doch sehr schwer. Ist es möglich, dass mir jemand von diesen 3 Parabeln die Scheitelpunktform und die allgemeine Form der Funktionsgleichung geben?

Es ist keine Hausaufgabe, ich versuche mir selbst den Stoff beizubringen, den ich über Corona verpasst habe.

Answer 4

Hallo

die allgemeine Form ist ja  y=a*(x-xs)²+ys

jetzt ist xs=0 bei allen 4. also hast du für die erste  y=ax²+25

jetzt kannst du noch die Nullstellen y(20)=0 also 0=a*400+25 und daraus a=-25/400=-1/16

allgemein kannst du auch sagen  wenn die Nullstelle x0 ist a=-ys/x0²

Damit sollte dir das für die 2 anderen leicht sein!

Gruß lul

Comments

Hallo, ich verstehe die Schreibweise leider nicht ganz.

---

Hallo

xs ist der x Wert des Scheitels, ys ist der y wert des Scheitels. Scheitel ist der höchst oder niedrigste Punkt.

Verstehst du es dann?

sonst sag bitte was du nicht verstehst.

Gruß lul

Answer 5

Die Parabel mit der Höhe h und der Breite b kannst du schreiben als

$$f(x)=h-\frac{h}{(\frac{b}{2})^2} \cdot x^2$$

Setzt mal h und b ein und vereinfache den Term.

Answer 6

Für die erste Funktion
( ganz ausführlich )
( x | y )
( 0 | 25 )
( 20 | 0 )
( -20 | 0 )

Normalform der Funktion
y ( x ) = a * x² + b * x + c
y ( 0 ) = a * 0² + b * 0 + c = 25
c = 25
y ( x ) = a * x² + b * x + 25

y (20 ) = a * 20² + b * 20 + 25 = 0
y (-20) = a * (-20)² + b * (-20) + 25 = 0

a * 20² + b * 20 + 25 = 0
a * (-20)² + b * (-20) + 25 = 0

a * 400 + b * 20 + 25 = 0
a * 400 - b * 20 + 25 = 0 | abziehen
------------------------------
b * 20 - ( - 20 * b ) =  0
40 * b = 0
b = 0

a * 20² + 0 * 20 + 25 = 0
a * 20² + 25 = 0
a * 400 = -25
a = - 1/16

Normalform
f ( x ) = -1/16 * x² + 25

Comments

Danke für die Antwort, ich verstehe allerdings die Schreibweise nicht ganz. Wofür * und /?

---

3 * 4 = 3 mal 4
3 / 4 = 3 durch 4

Ist allgemein so üblich

Answer 7

Hallo,

Scheitelpunkt bei ( 0|3)  Nullstellen bei (-1|0) und (1|0)

Scheitelpunktform f(x) = a(x-d)²+e   Scheitelpunkt einsetzen

                             f(x) = a( x-0) ² +3

                              f(x) = a x² +3      nun Nullstelle einsetzen

                                  0= a*1² +3       | -3

                                  -3= a

dann erhält man f(x) = -3 x²+3     das ist dann auch schon die Normalform