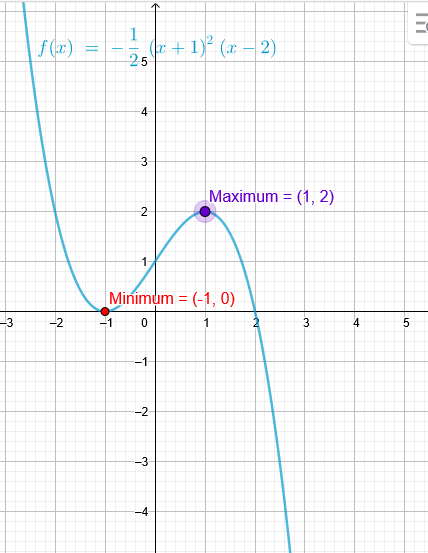
\((-1|0) Minimum und (1|2) Maximum\)
Nullstellenform der kubischen Parabel: Minimum bei (-1|0) bedeutet, dass dort eine doppelte Nullstelle ist.
\(f(x)=a*(x-(-1))^2*(x-N)=a*(x+1)^2*(x-N)\)
\((1|2) Maximum\):
\(f(1)=a*(1+1)^2*(1-N)=4a*(1-N)\)
\(4a*(1-N)=2→a=\frac{1}{2-2N}\)
\(f(x)=\frac{1}{2-2N}*[(x+1)^2*(x-N)]\)
In einem Maximum/Minimum haben wir eine waagerechte Tangente mit der Steigung \(m=0\)
\(f´(x)=\frac{1}{2-2N}*[2*(x+1)*(x-N)+(x+1)^2*1]\)
\(f´(1)=\frac{1}{2-2N}*[2*(1+1)*(1-N)+(1+1)^2]\)
\(f´(1)=\frac{1}{2-2N}*[4*(1-N)+4]\)
\(\frac{1}{2-2N}*[4*(1-N)+4=0]\)
\(N=2\) \(a=\frac{1}{2-2*2}=-\frac{1}{2}\)
\(f(x)=-\frac{1}{2}\)*(x+1)^2*(x-2)\)