Berechnen Sie die Maßzahl der Fläche(n) zwischen dem Graphen von \( f(x)=\frac{1}{4} x^{4}-2 x^{2}+10 \) und der Tangente in seinem Hochpunkt.
Bestimmung des Hochpunktes mittels Ableitung :
\( f'(x)=x^3-4x \)
\( x^3-4x=0 \) Satz vom Nullprodukt :
\( x(x^2-4)=0 \)
\( x_1=0 \) \( f(0)=10 \)
Die 2. Ableitung ist notwendig, um die Art des Extremwertes zu bestimmen:
\( f''(x)=3x^2-4 \)
\( f''(0)=-4<0 \) → Maximum
\( x^2=4 \)
\(x_2=2\) \( f(2)=6 \)
\(x_3=-2\) \( f(-2)=6 \)
\( f''(2)=8>0 \) → Minimum
Die Tangentensteigung durch Hochpunkte ( ebenso auch Tiefpunkte und Sattelpunkte) ist \(m=0\)
H\((0|10)\) führt zur Tangente \(y=10\)
Für die Flächenberechnung werden nun die Schnittpunkte der Tangente \(y=10\) mit \(f\) benötigt.
\( 10=\frac{1}{4} x^{4}-2 x^{2}+10 \)
\( \frac{1}{4} x^{4}-2 x^{2}=0|\cdot 4 \)
\( x^{4}-8 x^{2}=0 \) Wieder Satz vom Nullprodukt:
\( x^{2}(x^2-8 )=0 \)
\(x^2=8\)
\(x_1=\sqrt{8}= \sqrt{2\cdot 4}=2\sqrt{2}\)
\(x_2=-2\sqrt{2}\) (Symmetrie)
Zur Berechnung der Fläche(n) ein Bild der Graphen:
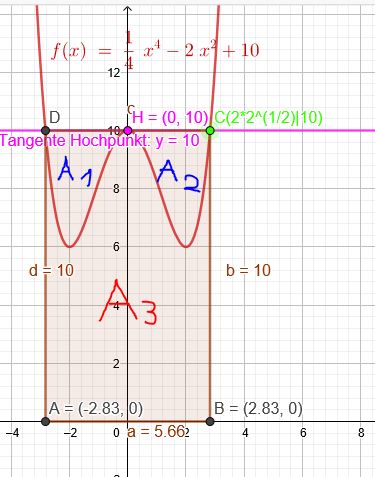
Die Flächen \(\blue{A_1}\) und \(\blue{A_2}\) haben gleiche Größe.
Das Rechteck A,B,C,D hat die Größe \(\red{A_3}\)
\(\red{A_3}=2\cdot 2\cdot \sqrt{2}\cdot 10 =40\cdot \sqrt{2}\)
Die Fläche unterhalb des Polynoms \(f\) hat die Größe:
\(2\cdot\int\limits_{0}^{2\cdot \sqrt{2}}(\frac{1}{4} x^{4}-2 x^{2}+10)dx\\=2\cdot [\frac{1}{20}x^5-\frac{2}{3}x^3+10x]_{0}^{2\cdot \sqrt{2}}\\=2\cdot [\frac{32}{20}\cdot 2^{\frac{5}{2}}-\frac{2}{3}\cdot 8\cdot 2^{\frac{3}{2}}+20\cdot \sqrt{2} ]-0\\=\frac{16}{5}\cdot 2^{\frac{5}{2}}-\frac{32}{3}\cdot 2^{\frac{3}{2}}+40\cdot \sqrt{2}\)
Diese Fläche muss nun von \(\red{A_3}\) abgezogen werden:
\( \red{40\cdot \sqrt{2}}-(\frac{16}{5}\cdot 2^{\frac{5}{2}}-\frac{32}{3}\cdot 2^{\frac{3}{2}}+40\cdot \sqrt{2})=\frac{16}{5}\cdot 2^{\frac{5}{2}}-\frac{32}{3}\cdot 2^{\frac{3}{2}} \)
Die gesuchte Fläche ist \(\blue{A_1} +\blue{A_2}=\frac{16}{5}\cdot 2^{\frac{5}{2}}-\frac{32}{3}\cdot 2^{\frac{3}{2}} \) FE groß.