Wie kann ich algebraisch prüfen, ob es sich um eine typische Umsatzfunktion handelt?

Question

Hallo :)

 

Ich habe eine Umsaztfunktion ( U(t)= -0,05t³+0,4t²+0,1t) gegeben.

Nun ist die Frage: Prufe ablebraisch, ob es sich um eine typische Umsatzfunktion handelt.

Mein Problem ich hab keinen blassen schimmer wie ich das machen muss :D

habt ihr eine Idee?

LG und

Answer 1

Eine Umsatzfunktion stellt den Zusammenhang zwischen Umsatz und Absatz (z. B. an Waren) dar.

Du kannst an der Funktion ablesen, welche Absatzmenge welchen Umsatz generiert.

Der Plot deiner Funktion sieht so aus (Absatz ist x-Achse, Umsatz ist y-Achse):

 

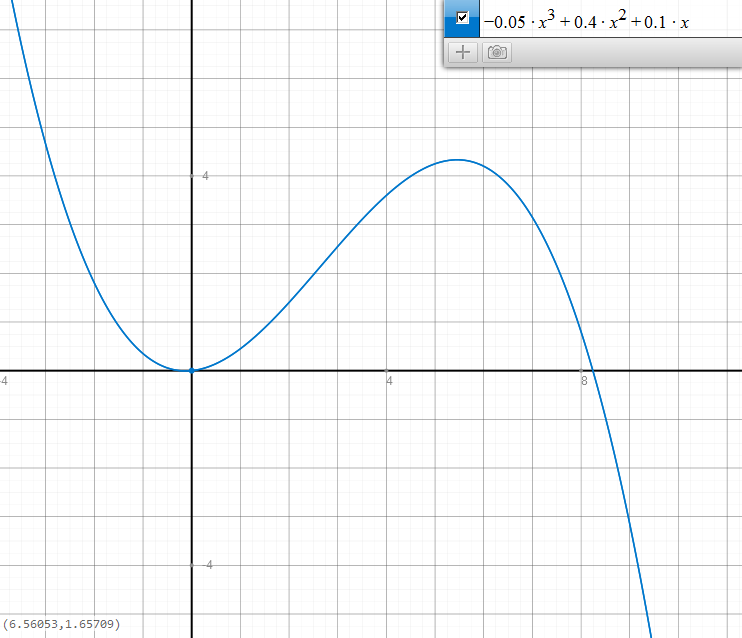
Betrachten wir nur den 1. Quadranten könnte dies unter Umständen eine Umsatzfunktion sein (Preis verändert sich mit abgesetzer Menge). Jedoch sind Umsatzfunktionen oft mit fixem Preis zu finden, also linear.

Mit "algebraisch prüfen" ist wahrscheinlich gemeint, dass du einige Werte einsetzt und überprüfst, ob diese dem Graphen einer Umsatzfunktion entsprechen.

 

Beispiele zweier Umsatzfunktionen:

 

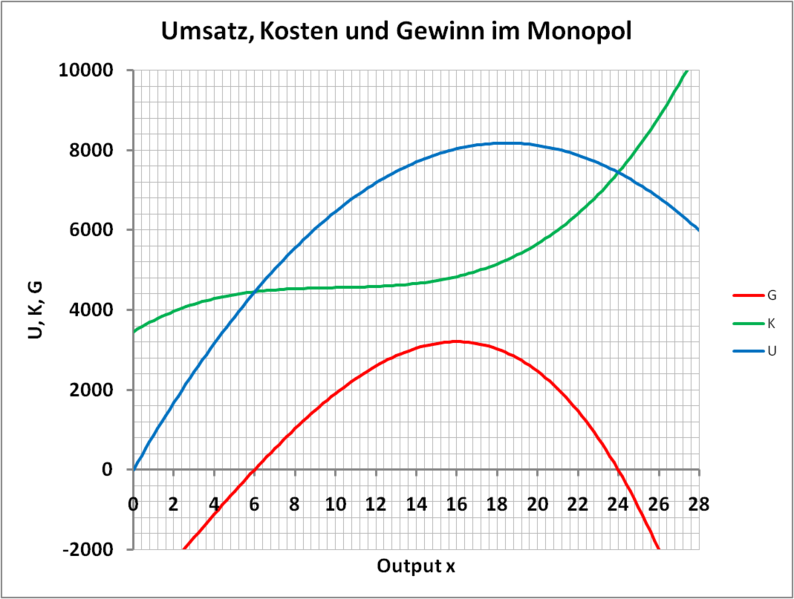
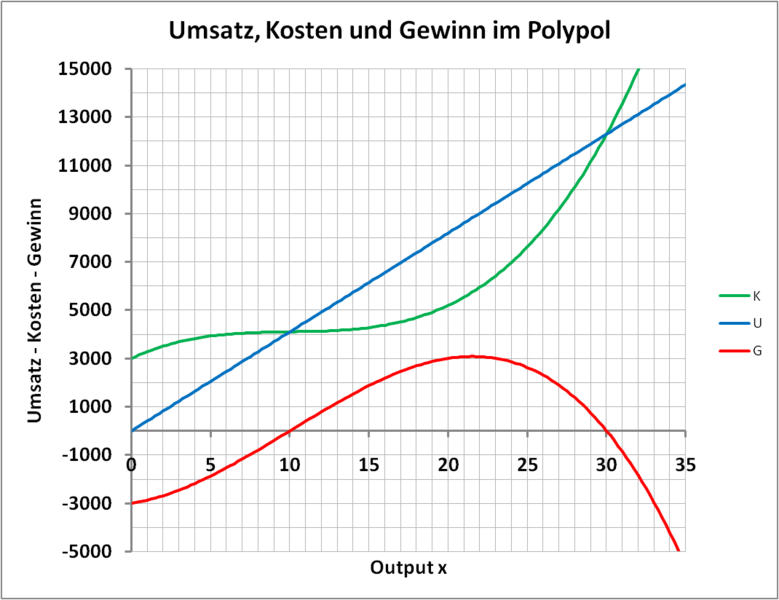
Bildlizenzen: ©Gabriele Hornsteiner CC by-sa

 

PS: Nicht die Preis-Absatz-Funktion mit der Umsatz-Absatz-Funktion verwechseln.

Comments

Kann es nicht sein dass hier einfach  "nur" um eine Kurvendikussion handelt, wobei man nachher die Beziehung zwischen Umsatz und Zeit ekennen muss.

---

Ja, das könnte man auch machen.
Da hier jedoch nach Algebra gefragt war, habe ich die Analysis außen vor gelassen.