Hallo,
ich möchte einen Beweis für die Rückrichtung angeben. Der ist nicht wirklich elegant, da er viele Fallunterscheidungen benutzt aber dafür recht anschaulich.
Seien also \(a,b,c,d\,>0\) reelle Zahlen, die die Ungleichungen erfüllen.
Fall 1: \(a+d>b+c\)
Fall 1.1: \(a\geq d\)
Erstmal eine kleine Skizze:
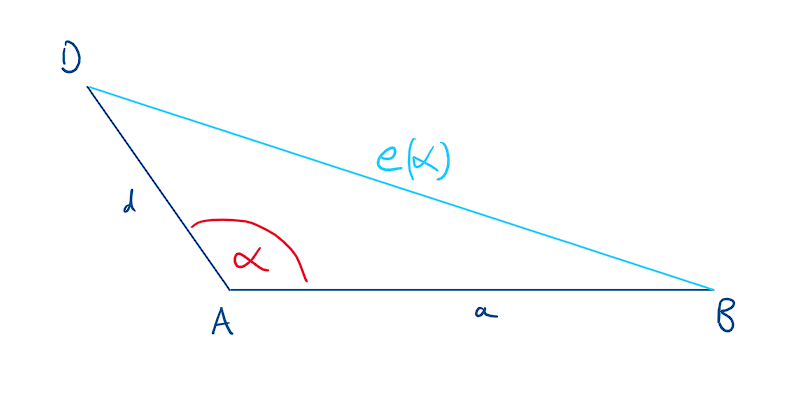
Wir können dabei \(\alpha\in(0,\pi)\) frei wählen und erhalten dann in Abhähngigkeit davon die Seite \(e=e(\alpha)\).Jetzt ist die Idee, dass wir an \(D\) einen Kreis von Radius \(c\) und an \(B\) einen Kreis vom Radius \(b\) zeichnen wollen. Wenn diese Kreise genau 2 Schnittpunkte haben, können den den "über" \(e\) als Eckpunkt \(C\) nehmen. Man kann sich klarmachen, dass das der Fall ist, falls $$\max(b,c)<e(\alpha)<b+c\tag1$$Finden wir also ein \(\alpha\in(0,\pi)\) sodass (1) gilt?
Nach Kosinussatz gilt \(e(\alpha)^2=a^2+d^2-2ad\cos(\alpha)\). Das ist sicherlich stetig in \(\alpha\) und wir erhalten \(e(0)=a-d\) (da \(d\leq a\)) und \(e(\pi)=a+d\). Nach Zwischenwertsatz gibt es also für jedes \(l\in(a-d,a+d)\) ein \(\alpha_l\) mit \(e(\alpha_l)=l\).
Nun ist nach Voraussetzung \(b+c<a+d\) und damit \(\max(b,c)<a+d\). Weiterhin ist \(a<b+c+d\) also \(a-d<b+c\).
Damit ist dann \((\max(b,c),b+c)\cap(a-d,a+d)\neq\emptyset\). Wir finden also ein \(\alpha_0\in(0,\pi)\) mit \(\max(b,c)<e(\alpha_0)<b+c\) und damit einen geeigneten Eckpunkt \(C\) als Schnittpunkt der Kreise:
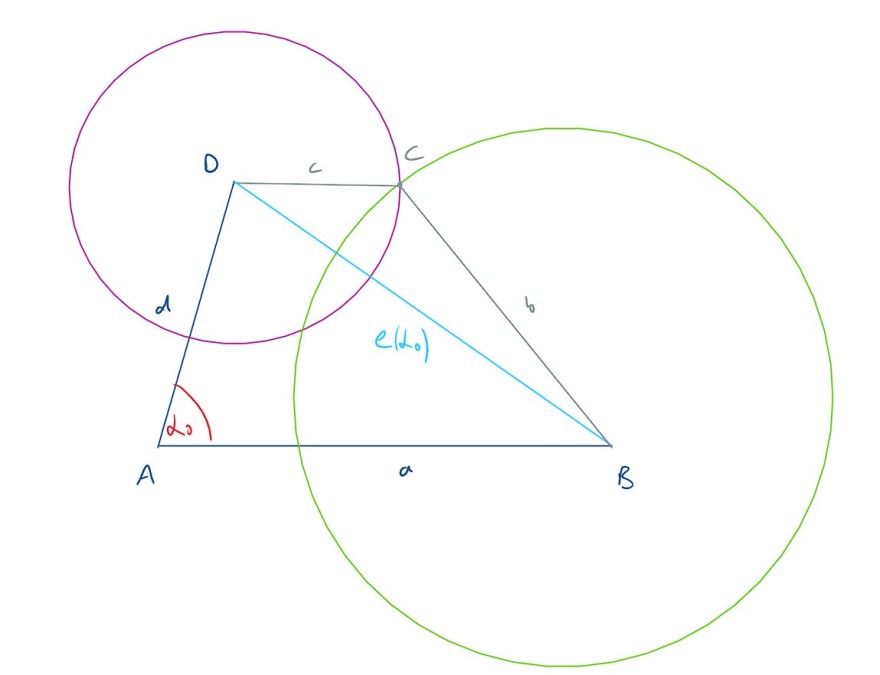
Nun gilt es noch die anderen Fälle abzuarbeiten.
Fall 1.2: a<d \(\rightarrow\) vertausche die Rollen von \(a\) und \(d\) in Fall 1.1
Fall 2: a+d<b+c \(\rightarrow\) Vertausche die Rollen von \(a,d\) mit \(b,c\) in Fall 1
Fall 3: a+d=b+c \(\rightarrow\) Falls auch \(a+b=c+d\) dann gilt \(a=c\) und \(b=d\) und wir können einfach das zugehörige Rechteck nehmen. Falls \(a+b\neq c+d\) gehe vor wie bei \(a+d\neq b+c\) in Fall 1 und 2.
Damit ist der Beweis abgeschlossen. Ich hoffe es hat sich kein Fehler eingeschlichen.
Wenn man etwas länger nachdenkt findet man bestimmt bessere Argumente um die Fälle ineinander zu überführen.
LG Dojima