Berechnen Sie den Flächeninhalt des grün markierten Bereichs zwischen x0=0 und x\max .

Question

Aufgabe:

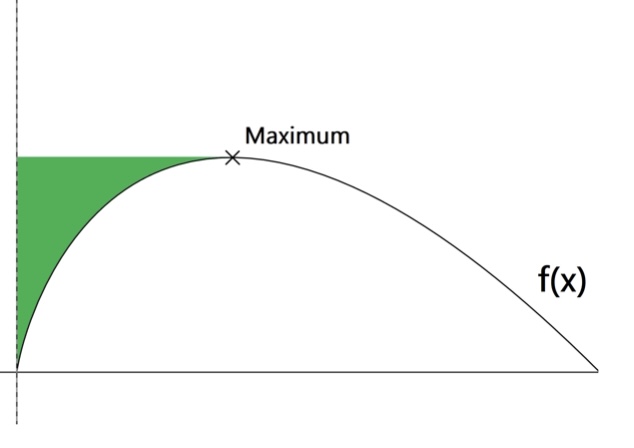
Berechnen Sie den Flächeninhalt des grün markierten Bereichs zwischen $x_{0}=0$ und $x_{\max }$. Die Funktionsvorschrift des eingezeichneten Graphen lautet $f(x)=-2 x \ln (3 x)$

Das Maximum befindet sich bei $x_{\max }=\frac{e^{-1}}{3}$
Der Flächeninhalt ergibt sich zu: ?

Text erkannt:

Berechnen Sie den Flächeninhalt des grün markierten Bereichs zwischen $x_{0}=0$ und $x_{\max }$. Die Funktionsvorschrift des eingezeichneten Graphen lautet $f(x)=-2 x \ln (3 x)$

Hinweis: Vereinfachen Sie ihr Ergebnis so weit wie möglich und geben Sie die analytische Lösung in das Antwortfeld ein.
Das Maximum befindet sich bei $x_{\max }=\frac{e^{-1}}{3}$
Der Flächeninhalt ergibt sich zu:

Problem/Ansatz:

Hallo zusammen, ich komme hier bei der Aufgabe nicht weiter. Beim Berechnen des Maximums gabs keine Probleme, jedoch beim Berechnen des Flächeninhalts, da der Graph nicht die y-Achse schneidet, obwohl man x0=0 benutzen soll. Kann mir hierbei jemand weiterhelfen. Vielen Dank im Voraus:)

Answer 1

Bei $x_0 = \frac{1}{3e}$ nimmt die Funktion ihr Maximum an, nämlich $f(x_0) = \frac{2}{3e}$ Der gesuchte Flcheninhalt ist also $$F = f (x_0) x_0 - \int_0^{x_0} f(x) dx$$

Dás Integral muss mittels partieller Integration gelöst werden. Da das Intehral an der unteren Grenze einen Wert von $\frac{\infty}{\infty}$ liefert, kann dieser Wert mittel L'Hospital bestimmt werden.

Bei mir kommt dann $$F = \frac{1}{18 e^2}$$ raus.

Answer 2

Mit einer Stammfunktion $F(x)$ ist der Flächeninhalt

  $x_\mathrm{max}\cdot f(x_\mathrm{max}) - (F(x_\mathrm{max}) - \lim\limits_{x\to 0} F(x))$.

Comments

Oder:$\int \limits_{0}^{e^{-1}/3}f(\frac{e^{-1}}{3})+2x\ln(3x)\, \mathrm{d}x$

Answer 3

f(x) = - 2·x·LN(3·x)
f'(x) = - 2·LN(3·x) - 2 = 0 --> x = 1/(3·e)

f(1/(3·e)) = 2/(3·e)

∫ (0 bis 1/(3·e)) (2/(3·e) + 2·x·LN(3·x)) dx = 1/(18·e²)