Berechnen Tangente e Funktionen

Question

Wie bestimmt man  die Gleichung der Tangente und Normale in $P(-1 \mid f(-1))$ und $Q(2 \mid f(2))$.

a) $f(x)=-e^{x}+5$
b) $f(x)=0,1 \cdot e^{x+6}$

Ich bedanke mich bei ihnen im Voraus.

Comments

War die Antwort .

Answer 1

hallo laura

einfach f'(-1) bestimmen und die Gerade durch P mit Steigung m=f'(-1) legen, entsprechend mit f'((2) und Q

Gruß lul

Comments

Hallo,

Gegeben ist ja P(-1| f(-1)

Die Y-Koordinate ist doch gegeben oder muss man das berechnen?

---

Die Y-Koordinate ist doch gegeben

Nein. f(-1) heißt nur:

y-Wert desjenigen Punktes des Funktionsgraphen, dessen x-Koordinate -1 ist.

---

Das heißt, um y der Formel y=m*x+n zu berechnen, muss ich die x-Koordinate in die Ausgangsfunktion einsetzen

f(-1)=y

ist das richtig?

Answer 2

Tangentengleichung:

t(x) = (x-x0)* f'(x0) + f(x0)

a) x = -1

f '(x) = -e^x

t(x) = (x+1)*(-e^(-1)) - e^(-1)+5

= ...

Die Normale hat die Steigung -1/f '(-1)

Answer 3

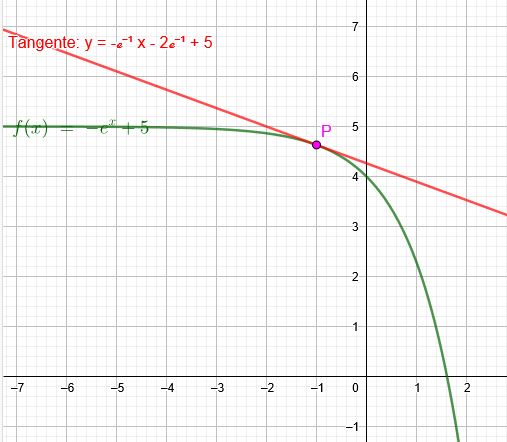
$f(x)=-e^{x}+5$

$f´(x)=-e^{x}$

$f´(-1)=-e^{-1}$

$P(-1|-e^{-1}+5)$

Punktsteigungsform der Tangente:

$\frac{y-(-e^{-1}+5)}{x-(-1)}=-e^{-1}$          $\frac{y+e^{-1}-5}{x+1}=-e^{-1}$

$y+e^{-1}-5=-e^{-1}*x-e^{-1}$

$y=-e^{-1}*x-2*e^{-1}+5$