Schwerpunkt der Fläche berechnen zwischen den Kurven y=1-(x-1)² und y=-√(1-(x-1)²)

Question

Berechnen sie den Schwerpunkt des Flächenstücks zwischen den Kurven

$$ y = 1 - ( x - 1 ) ^ { 2 } $$

und

$$ y = - \sqrt { 1 - ( x - 1 ) ^ { 2 } } $$

der Flächeninhalt beträgt 2,9.

Wie fange ich da an? Die beiden Funktionen gleichsetzen und dann nach 0 auflösen? Dann kommt aber ein x^4 heraus!

Answer 1

Ich zeichne mal die Fumnktion:

Aus Symmetriegründen befindet sich der Schwerpunkt schon mal auf einer Geraden durch x = 1.

Eine direkte Formel zur Bestimmung des Schwerpunktes finden wir unter:

https://de.wikipedia.org/wiki/Geometrischer_Schwerpunkt

Mit der Formel aus Wikipedia

ys = ∫ von a bis b über (f(x))^2 - (g(x))^2 dx / ∫ a bis b über 2*(f(x) - g(x)) dx

und

f(x) = 1 - (x - 1)^2
g(x) = - √(1 - (x - 1)^2)

errechne ich den Schwerpunkt wie folgt:

ys = ∫ von 0 bis 2 (1 - (x - 1)^2)^2 - (- √(1 - (x - 1)^2))^2 dx / ∫ von 0 bis 2 (2·(1 - (x - 1)^2 - - √(1 - (x - 1)^2))) dx

ys = - 4/15 / (3·pi + 8)/3 = - 4/(5·(3·pi + 8)) = -0.04591163237

Damit würde sich der Schwerpunkt etwas unterhalb der x-Achse befinden bei S(1 | -0.04591163237).

Comments

Hm, im Papula heisst die Formel für die Berechnung des Schwerpunktes aber:

$$ \frac { 1 } { A } \int _ { a } ^ { b } \int _ { f u } ^ { f o } y \; dy \; dx $$

Wie setze ich das dann ein. Muss ich erst die Funktionen nach Y umstellen?

Oder wie geht das?

---

Ja. Hier müsste die Umkehrfunktion gebildet werden. Das kann man aber umgehen. Schau mal auf das Beispiel:

https://de.wikipedia.org/wiki/Geometrischer_Schwerpunkt#Fl.C3.A4chenschwerpunkt_einer_Parabel

Man würde sich hier zu Nutze machen das sich der Schwerpunkt der beliebig kleinen Flächenstreifen  zwischen f(x) und g(x) berechnen lässt aus: (f(x) + (g(x))/2 dieses muss ich noch gewichten mit der Länge des Streifens. Die Länge des Streifens lässt sich berechnen aus f(x) - g(x).

Also wie in der Physik. Kraft * Kraftarm.

Das heißt wir könnten rechnen:

(f(x) + (g(x))/2 * (f(x) - g(x)) = (f(x)^2 - g(x)^2)/2

Damit umgeht man dann das Umformen zur Umkehrfunktion und es lässt sich sehr viel einfacher berechnen.

---

Danke, ich habe deine Formel auch im Papula gefunden und auch das richtige Ergebnis heraus bekommen!

Answer 2

Du fragst nach einem Anfang: Nicht nach der Formel zur Berechnung des Schwerpunktes (die findest du bestimmt in deinen Unterlagen): 

Du kannst erst mal die beiden Funktionen gleichsetzen, quadrieren, (1-x)^2 = u substituieren. Und eine quadr. Glg. für u lösen. Raus kommt, dass beide Funktionen dieselben Nullstellen haben: x₁ = 0 und x₂ = 2. 

Vgl. Abbildung:

 

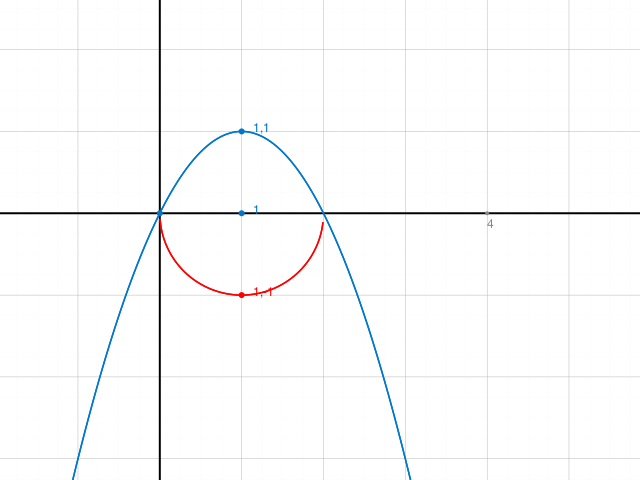
Aus Symmetriegründen ist die x-Koordinate des Schwerpunktes 1. Um die y-Koordinate zu bestimmen, integrierst du die (horizontalen Scheiben * Hebel) geschickt in y - Richtung: vgl. mit Unterlagen.