Integrieren mit Sinus, wie?

Question

Doppelintegration

Hey und zwar lerne ich gerade für Analysis 2 und mache die Hausaufgaben dieses Semesters, jedoch hatten wir solch eine Aufgabe nicht im letzten Semester und bin deshalb etwas überfragt wie man nach y integrieren soll..

Aufgabe:

Mein Ansatz:

x ∈ [0,2]

y ∈ [0,3]

$\int\limits_{0}^{3} [( \frac{1}{2}$ * x² * sin(y³)]₀² dy

$\int\limits_{0}^{3} [ 4( \frac{1}{2}$ * sin(y³) - 0 * sin(y³)]₀² dy

$\int\limits_{0}^{3} 2*sin(y^3)$ dy

? ab da komme ich nicht mehr weiter.

Vielen Dank schonmal im Voraus!!

Answer 1

Aloha :)

Willkommen in der Mathelounge... \o/

Bei dem Gebiet $G$ handelt es sich um ein Dreieck:

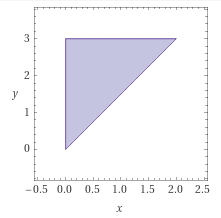
Deine Parametrisierung $(x\in[0;2]\;;\;y\in[0;3])$ beschreibt jedoch ein Rechteck. Daher muss die Menge $G$ zunächst korrekt parametrisiert werden. Die naheliegendste Parametrisierung ist, die Gerade $y=\frac32x$ als Untergrenze für die $y$-Werte anzusehen:$$G=\left\{(x;y)\in\mathbb R^2\,|\,0\le x\le2\;\land\;\frac32x\le y\le3\right\}$$Das würde aber bedeuten, dass wir zuerst über $dy$ bei festgehaltenem $x$ integrieren müssen und anschließend über $dx$ integrieren müssen. Das führt uns auf exakt dasselbe Problem, das du aktuell hast, nämlich das Integral von $\sin(y^3)$ zu bestimmen.

Zur Umgehung dieses Problems parametrisieren wir die Menge $G$ anders:$$G=\left\{(x;y)\in\mathbb R^2\,|\,0\le y\le3\;\land\;0\le x\le\frac23y\right\}$$Jetzt müssen wir nämlich zuerst über $dx$ bei festgehaltenem $y$ integrieren, wodurch das Integral sehr einfach wird:$$I=\iint\limits_G x\sin(y^3)\,dx\,dy=\int\limits_{y=0}^3\;\,\int\limits_{x=0}^{\frac23y} x\sin(y^3)\,dx\,dy=\int\limits_{y=0}^3\left[\frac{x^2}{2}\sin(y^3)\right]_{x=0}^{\frac23y}dy$$$$\phantom I=\int\limits_{y=0}^3\frac29y^2\sin(y^3)\,dy=\frac{2}{27}\int\limits_{y=0}^33y^2\sin(y^3)\,dy=\frac{2}{27}\left[-\cos(y^3)\right]_{y=0}^3$$$$\phantom I=\frac{2}{27}\left(-\cos(27)+\cos(0)\right)=\frac{2}{27}\left(1-\cos(27)\right)\approx0,0957$$Beachte, dass die Zahl $27$ im Argument des Cosinus keine Gradangabe ist.

Comments

Danke dir vielmals für die anschauliche Erklärung!! hast mir sehr weitergeholfen :)

---

Wie kamst du btw auf 3/2 bzw 2/3?

---

Für $y=0$ geht $x$ von $0$ bis $0$.

Für $y=3$ geht $x$ von $0$ bis $2$

Der linke Rand von $x$ ist immer $0$, der rechte Rand ist $\frac23y$ und wächst linear.