Wie kann ich hier die Richtungsableitung bestimmen?

Question

Aufgabe: Wie kann ich hier die Richtungsableitung bestimmen?

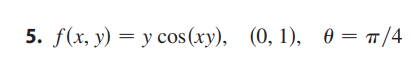
Text erkannt:

5. \( f(x, y)=y \cos (x y), \quad(0,1), \quad \theta=\pi / 4 \)

Problem/Ansatz:

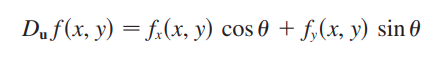
Text erkannt:

\( D_{\mathbf{u}} f(x, y)=f_{x}(x, y) \cos \theta+f_{y}(x, y) \sin \theta \)

Ich wollte diese Formel benutzen, aber komme nicht aufs richtige Ergebnis

Comments

Warum schreibst Du nicht hierhin, was Du gemacht hast.

---

Was sollen \((0,1)\) und \(\theta=\pi/4\) genau sein?

---

Oh sorry, Die Richtungsableitung soll bei dem Punkt (0,1) bestimmt werden und pi/4 ist der Winkel des unit vectors.

Answer 1

Aloha :)

Multipliziere den Gradienten im Punkt \((0;1)\) mit dem Richtungsvektor \(\binom{\cos\frac\pi4}{\sin\frac\pi4}=\frac{1}{\sqrt2}\binom{1}{1}\):$$D_{\varphi}f(0;1)=\operatorname{grad}f(0;1)\cdot\frac{1}{\sqrt2}\binom{1}{1}=\binom{-y^2\sin(xy)}{\cos(xy)-xy\sin(xy)}_{(0;1)}\cdot\frac{1}{\sqrt2}\binom{1}{1}$$$$\phantom{D_{\varphi}f(0;1)}=\binom{0}{1}\cdot\frac{1}{\sqrt2}\binom{1}{1}=\frac{1}{\sqrt2}\binom{0}{1}\binom{1}{1}=\frac{1}{\sqrt2}$$