Eine ganzrationale Funktion 3. Grades schneidet die y-Achse bei 4, berührt x-Achse bei 2, hat Wendepunkt bei x=1.

Question

Aufgabe:

Eine ganzrationale Funktion 3. Grades schneidet die y-Achse bei 4, berührt die xAchse bei 2 und hat einen Wendepunkt bei x=1. Gib die Funktionsgleichung an.

Problem/Ansatz:

Kann mir evtl jemand bei dieser Aufgabe helfen? Ich muss diese zu morgen auf Note bearbeiten, wir haben sowas allerdings noch nicht gemacht. Ich weiß einfach nicht, wie ich auf die Gleichung komme.

Vielen Dank im Voraus^^

Answer 1

Willkommen in der Mathelounge!

Eure Lehrkraft hat dir im Laufe des Abends eine Aufgabe gestellt, die du bis morgen bearbeiten sollst, ohne dass ihr das Thema im Unterricht besprochen habt? Das ist allerhand!

Eine "Bearbeitung auf Note" interpretiere ich dann als "Ich brauche die Lösung".

$f(x)=ax^3+bx^2+cx+d\\ f'(x)=3ax^2+2bx+c\\ f''(x)=6ax+2b\\[10pt] f(0)=4\quad \Rightarrow d =4\\ f(2)=0\quad \Rightarrow \quad 8a+4b+2c+4=0\\ f'(2)=0\quad \Rightarrow \quad 12a+4b+c=0\\ f''(1)=0\quad \Rightarrow \quad 6a+2b=0\\[10pt] f(x)=x^3-3x^2+4$

Gruß, Silvia

Answer 2

Eine ganzrationale Funktion 3. Grades schneidet die y-Achse bei 4, berührt die xAchse bei 2 und hat einen Wendepunkt bei x=1. Gib die Funktionsgleichung an.

Benutze zur Hilfe und Selbstkontrolle http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm

Eigenschaften

f(0) = 4
f(2) = 0
f'(2) = 0
f''(1) = 0

Gleichungssystem

d = 4
8a + 4b + 2c + d = 0
12a + 4b + c = 0
6a + 2b = 0

Errechnete Funktion

f(x) = x³ - 3·x² + 4

Skizze

Plotlux öffnen

f₁(x) = x³-3x²+4Zoom: x(-6…6) y(-2…6)

Answer 3

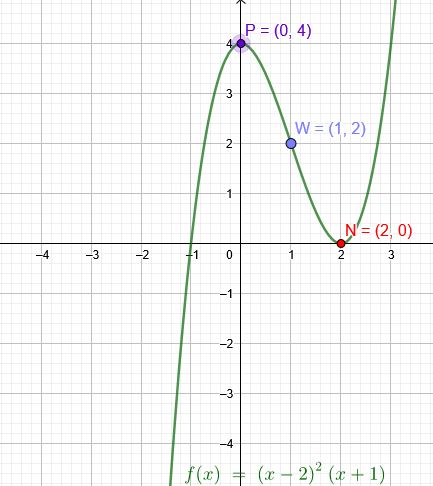
"Eine ganzrationale Funktion 3. Grades schneidet die y-Achse bei 4, berührt die x-Achse bei 2 und hat einen Wendepunkt bei x=1. Gib die Funktionsgleichung an."

berührt die x-Achse bei 2:

$f(x)=a*(x-2)^2*(x-N)$

schneidet die y-Achse bei 4:

$f(0)=a*(0-2)^2*(0-N)=-4*a*N=4$     →  $a=-\frac{1}{N}$

$f(x)=-\frac{1}{N}*[(x-2)^2*(x-N)]$

hat einen Wendepunkt bei x=1:

$f´(x)=-\frac{1}{N}*[(2x-4)*(x-N)+(x-2)^2*1]$

$f´´(x)=-\frac{1}{N}*[(2x-2N)+(2x-4)*1+(2x-4)*1]$

$f´´(1)=-\frac{1}{N}*[(2*1-2N)+(2*1-4)+(2*1-4)]=0$   →  $N=-1$     →  $a=1$

$f(x)=(x-2)^2*(x+1)$