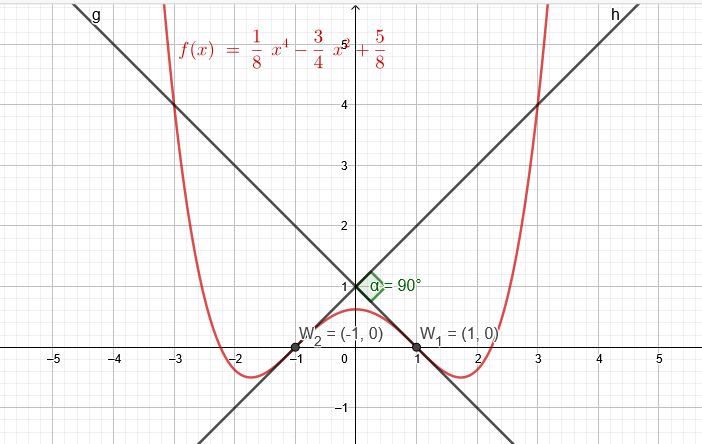
Bestimmen sie alle ganzrationalen Funktionen vom Grad vier mit zur y-Achse symmetrischen Graphen.

Question

Aufgabe:

Bestimmen sie alle ganzrationalen Funktionen vom Grad vier mit zur y-Achse symmetrischen Graphen. Ein Wendepunkt ist W(1/0). Die beiden Wendetangenten schneiden sich senkrecht.

Problem/Ansatz:

Bis zum Wendepunkt hab ich es verstanden. Aber den letzten Schritt versteh ich leider nicht ganz. Könnte mir den vielleicht jemand erklären?

Answer 1

Bestimmen sie alle ganzrationalen Funktionen vom Grad vier mit zur y-Achse symmetrischen Graphen. Ein Wendepunkt ist W(1|0). Die beiden Wendetangenten schneiden sich senkrecht.

Ein Wendepunkt ist $W_1(1|0)$  Wegen der Symmetrie gilt auch $W_2(-1|0)$

Allgemein 4.Grad: $f(x)=a*x^4+b*x^3+c*x^2+d*x+e$

hier: $f(x)=a*x^4+c*x^2+e$

$W_1(1|0)$

$f(1)=a+c+e$

1.)    $a+c+e=0$

$W_1(1|...)$

$f´(x)=4a*x^3+2c*x$

$f´´(x)=12a*x^2+2c$

$f´´(1)=12a+2c$

2.)    $12a+2c=0$    →   $c=-6a$

Die beiden Wendetangenten schneiden sich senkrecht:

$f´(1)=4a+2c$   →  $f´(1)=4a+2*(-6a)$  →  $f´(1)=-8a$ 

$f´(-1)=4a*(-1)^3+2c*(-1)=-4a-2*(-6a)=-4a+12a=8a$

Orthogonal: $m_2*m_1=-1$

$-8a*8a=-1$  → $64a^2=1$   → $a_1=\frac{1}{8}$   $a_2=-\frac{1}{8}$

Mit   $a_1=\frac{1}{8}$ weiter:  $c=-6*\frac{1}{8}$  → $c=-\frac{3}{4}$ 

1.)    $a+c+e=0$  →   $\frac{1}{8}-\frac{3}{4}+e=0$  →  $e=\frac{5}{8}$

$f(x)=\frac{1}{8}*x^4-\frac{3}{4}*x^2+\frac{5}{8}$

Du musst nun noch die weitere Funktion mit $a_2=-\frac{1}{8}$ bestimmen.

Comments

Dankeschön:) Sie haben mir echt weitergeholfen!

Answer 2

f(x) = ax⁴+bx²+c

f(1) =0

f''(1) = 0

senkrecht schneiden heißt: m1*m2= -1

m1, m2 = Steigung der Wendetangenten im WP

Tangentengleichung:

t(x) = (x-1)*f'(1) + f(1)

Comments

Vielen Dank Ihnen!

Answer 3

Die beiden Wendetangenten schneiden sich senkrecht.

Das bedeutet ja, dass das Produkt der Ableitungen an den beiden Wendestellen $-1$ ergeben muss. Dies ergibt die Bedingung $$f'(-1)\cdot f'(+1)=-1.$$ Die beiden anderen Bedingungen, die benötigt werden, sind dir ja bekannt.

Comments

Vielen Dank Ihnen!