quadratische Gleichung Aufgabe Frage…….

Question

Berechne die Zahl x.
x2+x=90
Frage: Rechnet man die Aufgabe mit quadratischer Ergänzung????

Answer 1

 

ich würde es mit der pq-Formel berechnen:

x² + px + q = 0

x_1,2 = -p/2 ± √[(p/2)² - q]

 

x² + x = 90 | -90

x² + x - 90 = 0 | jetzt ist p = 1 und q = -90

x_1,2 = -1/2 ± √(1/4+90) = -1/2 ± √(361/4) = -1/2 ± 19/2

x₁ = 18/2 = 9

x₂ = -20/2 = -10

 

Probe:

81 + 9 = 90 | stimmt

100 - 10 = 90 | stimmt

 

Besten Gruß

Comments

danke :),aber man kann es auch mit der quadratischen Ergänzung rechen oder?gruß.

---

Ich weiß nicht, ob das soviel bringt, denn die quadratische Ergänzung ist eine Technik, um einen quadratischen Term umzuformen und in die Scheitelpunktform zu bringen:

x² + x = 90 | - 90

x² + x - 90

(x² + x) - 90 | (p/2)² addieren und sofort wieder subtrahieren

(x² + x + 1/4 - 1/4) - 90

(x² + x + 1/4) - 1/4 - 90 | 1. Binomische Formel

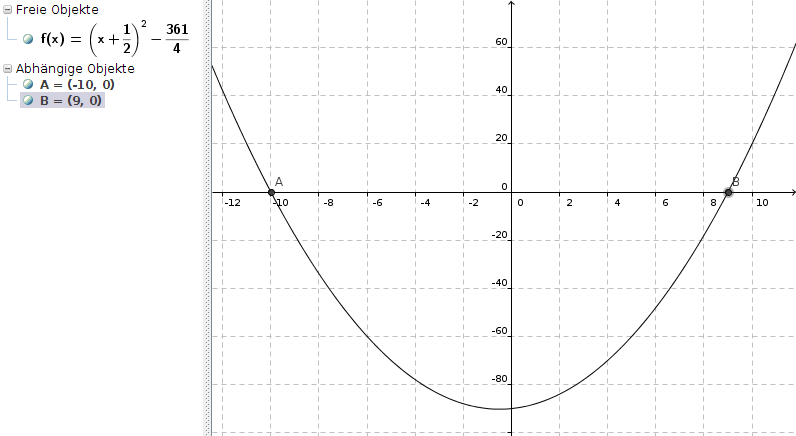
(x + 1/2)² - 361/4

Jetzt siehst Du, dass das Minimum der Funktion bei (-1/2|-361/4) liegt, aber die Nullstellen kannst Du aus diesem Term nicht direkt herauslesen:

---

Hier bietet sich wirklich an die pq-Formel anzuwenden. Aber wenn die quadratische Gleichung schon in Scheitelpunktform vorliegt kann man daraus direkt die Nullstellen ermitteln.

https://de.wikipedia.org/wiki/Scheitelpunkt#Bestimmung_der_Nullstellen_aus_der_Scheitelpunktform.

---

Danke sigma,

wieder was gelernt :-)