f(x) = (x^2 - 2·x)·e^{0.5·x}
a) begründen sie das f nicht symmetrisch ist
f(1) = - e^{1/2}
f(-1) = 3·e^{- 1/2}
f(-1) ≠ f(1)
f(-1) ≠ -f(1)
b) untersuchen sie die Funktion auf nullstellen. Geben sie Achsenschnittpunkts an
Y-Achsenabschnitt f(0)
f(0) = 0 --> Gleichzeitige Nullstelle
Nullstellen f(x) = 0
(x^2 - 2·x) = 0
x = 2 ∨ x = 0
c) betrachten sie dass verhalten der Funktion Im unendlichen
lim (x --> -∞) f(x) = 0+
lim (x --> ∞) f(x) = ∞
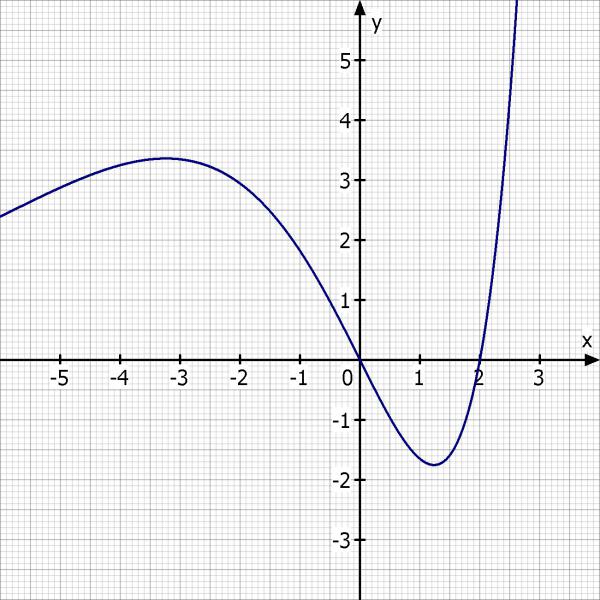
Skizze