Textaufgabe, quadratische Funktionen: Rotierende Flüssigkeit in Zylinder.

Question

In Zylinderförmigen Behältern rotierende Flüssigkeiten bilden im Querschnitt Parabelförmige Oberflächen. Bestimme die Gleichung der Parabel, wenn bei 12 cm Durchmesser zwischen dem Rand der Flüssigkeit und der tiefsten Stelle 5,6 cm Unterschied sind.

Answer 1

annahme das der tiefstePunkt bei der rotation der Boden ist .

bei einen wert von  6 ist die Höhe dann 5,6

x=6 und y= 5,6

 die allemeine Form der Parabel ist

f(x= ax²+bx+c                        b=0 und c=0

 Die Werte von oben einsetzen und  den parameter a berechnen:

5,6= a*36          a= 0,155555

Die Funktion lautet :

f(x)=0,15555 x²

 

 

 

Answer 2

 

Akelei hat es ja schon gemacht. Ich persönlich verwende allerdings noch eine etwas andere, in meinen Augen leichtere, Methode.

Wir erinnern uns an die Steigung einer Geraden. Die war definiert aus

m = Δy / Δx = (Py - Qy) / (Px - Qx)

wenn wir die Steigung zwischen den Punkten P(Px | Py) und Q(Qx | Qy) errechnen. Die Öffnung einer Parabel hat zufällig eine ähnliche Form

a = Δy / (Δx)^2 = (Py - Sy) / (Px - Sx)^2

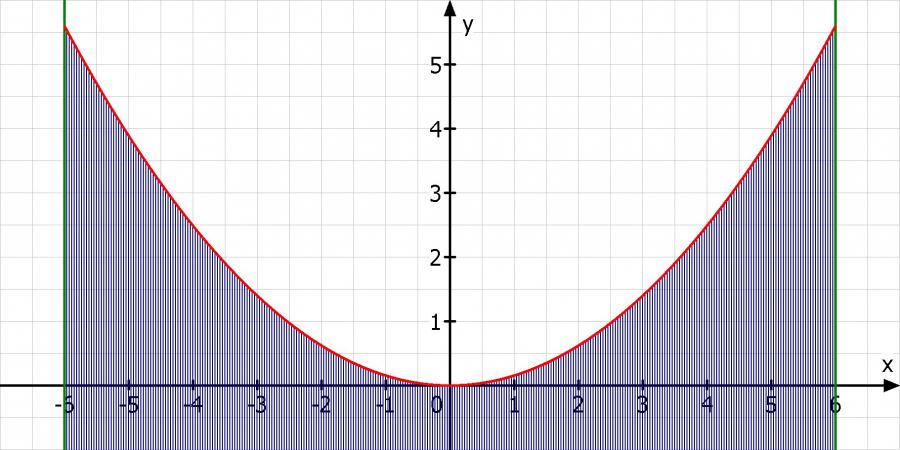
Hier berechnen wir die Öffnung der Parabel zwischen dem Scheitelpunkt S(Sx | Sy) und einen weiteren Punkt P(Px | Py) der Parabel.

In Deinem Beispiel sehe die Berechnung wie folgt aus:

a = Δy / (Δx)^2 = (Py - Sy) / (Px - Sx)^2 = 5,6 / 6^2 = 7/45

Die Parabel hat also die Funktionsgleichung

f(x) = 7/45 x^2