Ungleichung mti vollständiger Induktion zeigen

Question

Ich hätte nur eine Frage bzgl. einer Umformung. Seien a_1, . . . , a_n ≥ 0 und n ∈ N. Sei a_n+1 ≥ 0. Es soll folgende Ungleichung gezeigt werden

Text erkannt:

\( \left(\frac{\sum \limits_{k=1}^{n+1} a_{k}}{(n+1) \cdot \bar{a}_{n}}\right)^{n+1} \geq \frac{a_{n+1}}{\bar{a}_{n}} \)

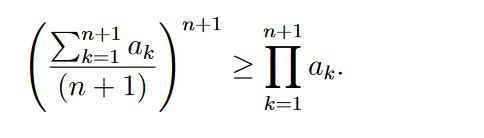
Text erkannt:

\( \left(\frac{\sum \limits_{k=1}^{n+1} a_{k}}{(n+1)}\right)^{n+1} \geq \prod \limits_{k=1}^{n+1} a_{k} \)

Um diese zu beweisen soll die Induktionsvoraussetzung und folgende Ungleichung verwendet werden

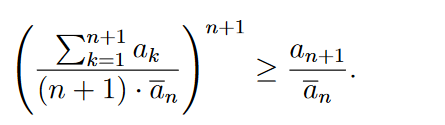
Text erkannt:

\( \left(\frac{\sum \limits_{k=1}^{n+1} a_{k}}{(n+1) \cdot \bar{a}_{n}}\right)^{n+1} \geq \frac{a_{n+1}}{\bar{a}_{n}} \).

Also, Induktionsvoraussetzung ist hier (∑ⁿ_k=1 a_k )/n))ⁿ ≥∏ⁿ_k=1 a_k. Also einfach für "n+1" "n" eingesetzt. Nun zum Induktionsschritt. Wie forme ich nun den Ausdruck:

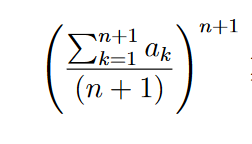
Text erkannt:

\( \left(\frac{\sum \limits_{k=1}^{n+1} a_{k}}{(n+1)}\right)^{n+1} \)

so um, dass ich die Induktionsvoraussetzung verwenden kann bzw. mti der anderen Ungleichung abschätzen kann?

Answer 1

Mit ist nicht ganz klar, was Du fragst. Es scheint doch alles Nötige beisammen. Wenn ich zur Abkürzung das arithmetische Mitte der a_k von 1 bis n mit \(p_n\) bezeichne, dann ist doch folgende Ungleichung von Dir zitiert und in Deinem vorigen Post. bewiesen worden:

$$\left( \frac{p_{n+1}}{p_n}\right)^{n+1} \geq \frac{a_{n+1}}{p_n} \iff p_{n+1}^{n+1} \geq a_{n+1}p_n^n \quad (1)$$

Induktionsannahme ist: Frü ein natürliches n gilt
$$\prod_{k=1}^na_k \leq p_n^n$$

Damit folgt mit der Induktionsannahme und (1)

$$\prod_{k=1}^{n+1}a_k= a_{n+1} \prod_{k=1}^na_k \leq a_{n+1}p_n^n\leq p_{n+1}^{n+1}$$

Answer 2

Schau mal dort:

https://www.mathelounge.de/1066888/zeigen-sie-mit-hilfe-der-bernoull…

Comments

Sind die Umformungen etwa ähnlich?