Aufgabe:
a) Eine Münze wird sechsmal geworfen. Mit welcher Wahrscheinlichkeit fallen folgende Ereignisse?
1) genau dreimal Wappen
2) weniger als dreimal Wappen
3) mehr als dreimal Wappen
b) Wie ändern sich die Wahrscheinlichkeiten, wenn die Wahrscheinlichkeit für Wappen etwas grö-
ßer als \( \frac{1}{2} \) ist?
c) Kontrollieren Sie Ihre Rechnungen aus a) und b) mit einem Rechenhilfsmittel.
Ansatz:
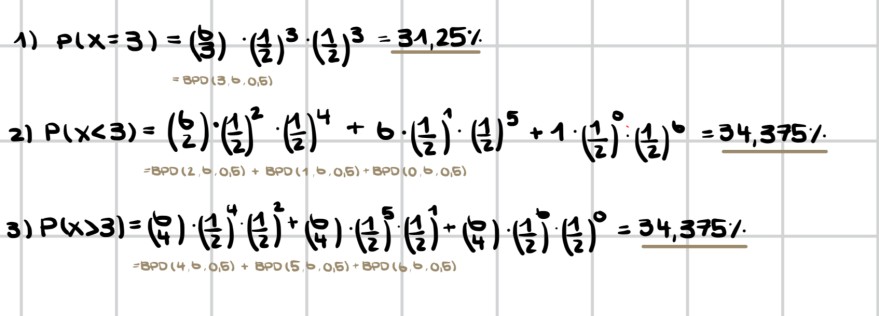
Text erkannt:
1) \( p(x=3)=\left(\frac{6}{3}\right) \cdot\left(\frac{1}{2}\right)^{3} \cdot\left(\frac{1}{2}\right)^{3}=31,25 \% \)
2) \( P(x<3)=\binom{6}{2} \cdot\left(\frac{1}{2}\right)^{2} \cdot\left(\frac{1}{2}\right)^{4}+6 \cdot\left(\frac{1}{2}\right)^{1} \cdot\left(\frac{1}{2}\right)^{5}+1 \cdot\left(\frac{1}{2}\right)^{0} \cdot\left(\frac{1}{2}\right)^{6}=34,375 \% \)
3) \( P(x>3)=\binom{6}{4} \cdot\left(\frac{1}{2}\right)^{4} \cdot\left(\frac{1}{2}\right)^{2}+\binom{6}{4} \cdot\left(\frac{1}{2}\right)^{5} \cdot\left(\frac{1}{2}\right)^{1}+\binom{6}{4} \cdot\left(\frac{1}{2}\right)^{6} \cdot\left(\frac{1}{2}\right)^{0}=34,375 \% \)
\( =B P D(4,0,0,5)+B P D(5,0,0,5)+B P D(6,6,0,5) \)
Ich würde sagen dass die Wahrscheinlichkeiten steigen, falls die Wahrscheinlichkeit über 0,5 liegt.
Kann mir jemand einen Feedback zu meine Lösung geben? Ich müsste eigentlich auch die Aufgabe 4a ohne Taschenrechner berechnen. Wie geht das??