Aufgabe:
Ich würde gerne wissen, wieso man nach \( \frac{2bc^{2}}{c-2} \)nicht weiter vereinfachen kann.
Problem/Ansatz:
Bei der zweiten Rechnung konnte ich alle Variablen über und unter dem Bruchstrich beseitigen, die gleich waren. Ich glaube, dass wohl die -2 von c-2 weiteres verhindert. Womöglich, weil es gegen ein Mathegesetz verstößt (Kommutativ/Distributiv)? Bei der zweiten Rechnung konnte ich es ohne weiteres, weil es kein +/- gab(?).
Außerdem war ich der festen Überzeugung, dass z.B 27\( x^{6} \)eine feste Einheit ist, aber anscheinend kann es genau so gut 27\( y^{3} \) sein (Ich beziehe mich auf \( \frac{27x^{6}...}{9x^{3}...} \) ), weil das Kommutativgesetz es erlaubt(?).
Hoffentlich könntet ihr meine Verwirrung auflösen, vielen Dank im Voraus!
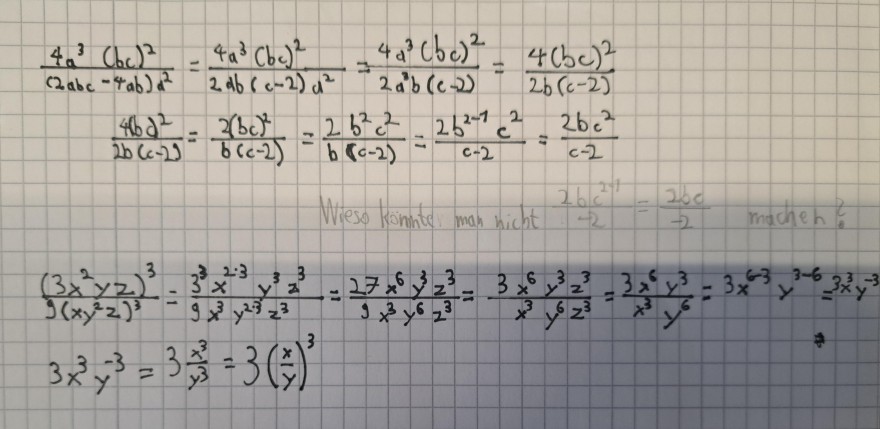
Text erkannt:
\( \begin{aligned} \frac{4 a^{3}(b c)^{2}}{(2 a b c-4 a b) a^{2}} & =\frac{4 a^{3}(b c)^{2}}{2 a b(c-2) a^{2}}=\frac{4 a^{3}(b c)^{2}}{2 a^{3} b(c-2)}=\frac{4(b c)^{2}}{2 b(c-2)} \\ \frac{4 b d^{2}}{2 b(c-2)} & =\frac{2(b c)^{2}}{b(c-2)}=\frac{2 b^{2} c^{2}}{b(c-2)}=\frac{2 b^{2-1} c^{2}}{c-2}=\frac{2 b c^{2}}{c-2} \end{aligned} \)
\( \begin{array}{l} \frac{\left(3 x^{2} y z\right)^{3}}{9\left(x y^{2} z\right)^{3}}=\frac{3^{3} x^{2 \cdot 3} y^{3} z^{3}}{9 x^{3} y^{2 \cdot 3} z^{3}}=\frac{27 x^{6} y^{3} z^{3}}{9 x^{3} y^{6} z^{3}}=\frac{3 x^{6} y^{3} z^{3}}{x^{3} y^{6} z^{3}}=\frac{3 x^{6} y^{3}}{x^{3} y^{6}}=3 x^{6-3} y^{3-6}=3 x^{3} y^{-3} \\ 3 x^{3} y^{-3}=3 \frac{x^{3}}{y^{3}}=3\left(\frac{x}{y}\right)^{3} \end{array} \)