Bestimmen Sie rechnerisch die Ecken und Kanten des folgenden Polyeders

Question

Aufgabe:

Bestimmen Sie rechnerisch die Ecken und Kanten des folgenden Polyeders

\( P=\left\{x \in \mathbb{R}^{3}: \quad \begin{array}{rl} x_{1}-x_{2}+x_{3} & \leq 10 \\ 2 x_{1}-x_{2}+2 x_{3} & \leq 40 \\ 3 x_{1}-2 x_{2}+3 x_{3} & \leq 50 \\ x_{1}, x_{2}, x_{3} & \geq 0 \end{array}\right\} \)

Problem/Ansatz:

Mag mir jemand bei der Aufgabe helfen? Weiß leider nicht so wirklich wie das geht.

Comments

Hallo. Ich weiß auch nicht, wie das geht, aber ich sehe sechs Ebenengleichungen, die den (oder das?) Polyeder begrenzen.

---

das Polyeder, behauptet Duden

Bei einer Kante schneiden sich zwei Ebenen, bei einem Punkt drei.

---

Hatte das mal so probiert aber das scheint falsch zu sein:

Text erkannt:

0.

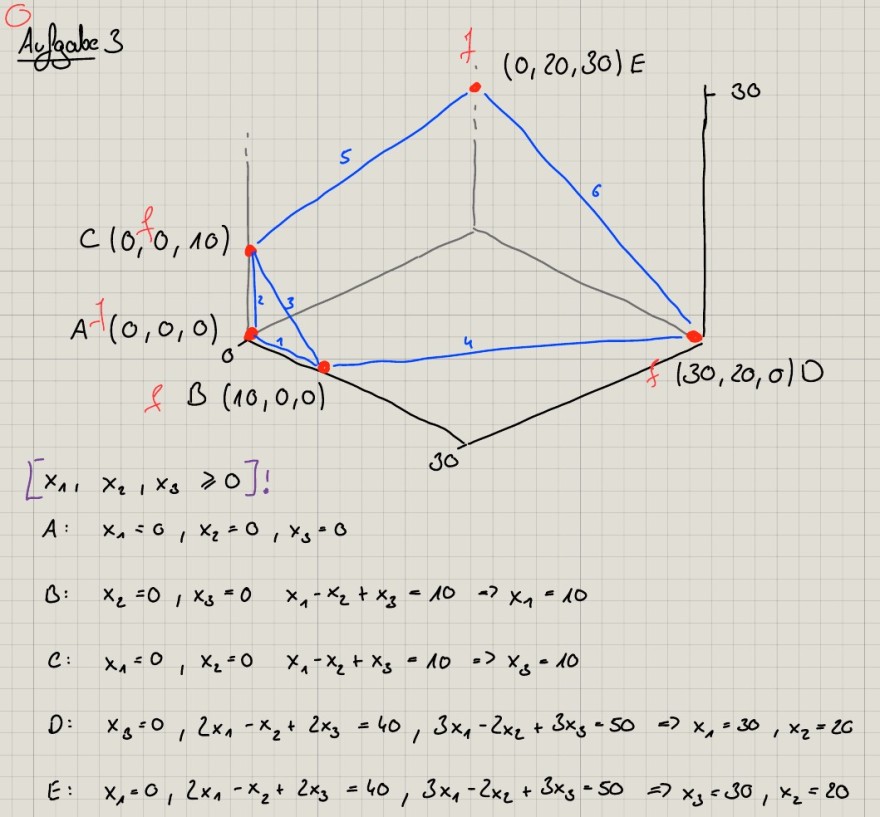
Auggabe 3
\( \begin{array}{l} {\left[x_{1}, x_{2}, x_{3} \geqslant 0\right]!} \\ A: x_{1}=0, x_{2}=0, x_{3}=0 \\ B: x_{2}=0, x_{3}=0 \quad x_{1}-x_{2}+x_{3}=10 \Rightarrow x_{1}=10 \\ C: x_{1}=0, x_{2}=0 \quad x_{1}-x_{2}+x_{3}=10 \Rightarrow x_{3}=10 \\ D: x_{3}=0,2 x_{1}-x_{2}+2 x_{3}=40,3 x_{1}-2 x_{2}+3 x_{3}=50 \Rightarrow x_{1}=30, x_{2}=20 \\ E: x_{1}=0,2 x_{1}-x_{2}+2 x_{3}=40,3 x_{1}-2 x_{2}+3 x_{3}=50 \Rightarrow x_{3}=30, x_{2}=20 \end{array} \)

---

Was auffällt, ist das Gleichung 3 die Summe von 1 und 2 ist, also redundant

---

Die dritte Bedingung folgt aus den beiden ersten (summiere diese). Du kannst also die dritte Bedingung einfach weglassen.

Weiter ist das Ganze kein geschlossenes Polyeder. Setze zum Beispiel \(x_1=x_3=4\) und dann \(x_2 = a > 0 \). Dann sind alle Bedingungen immer erfüllt, egal wie groß man \(a\) wählt. Folglich hat die so beschriebenen Menge kein endliches Volumen und ist daher auch kein Polyeder.

Prüfe bitte, ob Du die Bedingungen korrekt abgeschrieben hast.

---

Ja genau, es gibt drei unbegrenzte Strahlen, z.B. die gesamte positive x₂-Achse

---

Hier ein Screenshot. Anscheinend ist die Aufgabe also Quatsch? Oder versteh ich da was falsch.

---

Der Screenshot war ja vorher in der Frage vorhanden. Hat der liebe Moderator nur mal wieder unnötigerweise entfernt.

---

Anscheinend ist die Aufgabe also Quatsch? Oder versteh ich da was falsch.

Na ja, ein klassisches (beschränktes) Polyeder ist das jedenfalls nicht.

Wenn die Aufgabe hingegen aus dem Bereich der Linearen Optimierung stammt, dann könnte es so gewollt sein, da wird der Begriff anders benutzt und erlaubt auch unbeschränkte Objekte.

---

Das ist eine Aufgabe aus der Linearen Optimierung. Was wäre dann meine vorgehensweise?

---

Die zulässigen Basislösungen entsprechen den Ecken des Polyeders.

---

Hatte das mal so probiert aber das scheint falsch zu sein:

Nein - ist es nicht. Du hast alle fünf Eckpunkte gefunden. Es fehlen lediglich die Kanten die 'in's Unendliche' abhauen. Berechne dazu die Schnittgerade der Ebene $$2x-y+2z=40$$ mit den Ebenen \(x=0\) und \(z=0\).

Ein wenig 3D-Vorstellung schadet dabei nicht: