Berechne den Flächeninhalt, der auf [-1,3] von f(x) = l x - 2 l und g(x) = l x l + 1 eingeschlossen wird

Question

Aufgabe:

Berechne den Flächeninhalt, der auf dem Intervall [-1,3] von den Funktionen f(x) = l x - 2 l und g(x) = l x l + 1 eingeschlossen wird.

Problem/Ansatz:

Ich komme beim Integral auf -12, also 12 als Fläche. Die Lösung soll aber 6,5 sein?

Comments

Liefere deine Rechnung mit, damit man auch nach deinem Fehler suchen kann.

---

Schiebe die hellen Flächen zu den dunklen Flächen derselben Farbe.

Dann erhält man, von links nach rechts, die quadratischen bis rechteckigen Flächen mit 4 (grün), 1 (rot), 9 (blau) und 12 (braun) Karos. Da ein Karo einen Flächeninhalt von 1/4 hat, ist die Lösung (4+1+9+12) / 4 = 6,5

(Zeichnung basiert auf der Skizze vom Apfelmännchen, cf. unten.)

---

wir sollen es mit Integral machen

---

Wie schon gesagt: ohne deine Rechnung lässt sich nicht nachvollziehen, wo dein Fehler liegt.

---

wir sollen es mit Integral machen

Das steht nicht in der Aufgabe, bzw. hast Du verschwiegen.

Immerhin beantwortet die Zeichnung Deine Problembeschreibung "Die Lösung soll aber 6,5 sein?" Ja, ist sie, wie man anhand der Quadrate und des Rechtecks unmittelbar nachvollziehen kann.

Answer 1

Ich komme beim Integral auf -12, also 12 als Fläche. Die Lösung soll aber 6,5 sein?

Du hast vermutlich direkt die Beträge in den Funktionen ignoriert.

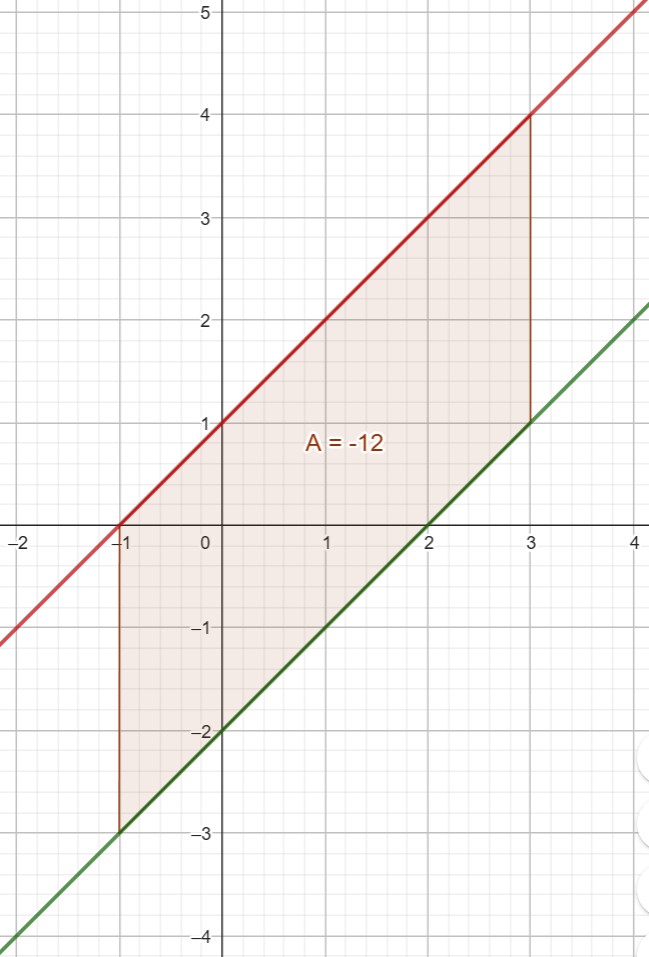
Es sollte aber eher wie folgt aussehen:

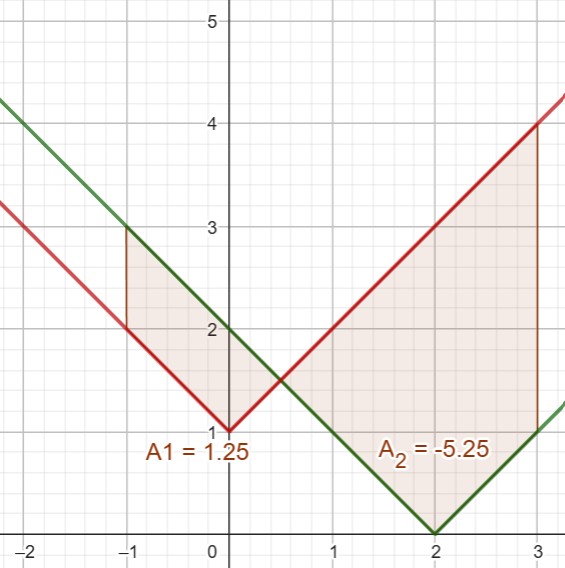
Zum Zeichnen ist es günstig, wenn man weiß, dass

f(x) die Betragsfunktion ist, die um 2 Einheiten nach rechts verschoben wurde und dass

g(x) die Betragsfunktion ist, die um 1 Einheit nach oben verschoben wurde.

Rechnerisch kann man es über eine Fallunterscheidung machen.

Comments

Das wars, aber mit den Strichen komme ich leider nicht klar.

Answer 2

Die Lösung ist korrekt und man kommt hier sogar komplett ohne Integralrechnung aus, da man nur eckige Flächen zusammenrechnen muss: