Festlegung von Konvertierungsregeln in der Mathematik als Ersatz für die Integralrechnung

Question

Aufgabe:

Festlegung von Konvertierungsregeln in der Mathematik als Ersatz für die Integralrechnung

Problem/Ansatz:

Informatik: Konvertierung einer Ausgangsbewegung mit dem Ergebnis einer Animation im Browser (Bewegungsablauf)

http://www.wichmann.dashosting.de/Pest/Pest.html

Produktionstechnik / Physik: Bewegungsablauf berechnen  s(t)=∫v(t)dt+s₀ bzw. v(t)=∫a(t)dt+v₀

Der von mir im Link angegebene Bewegungsablauf eines Iframes kann doch verglichen werden mit dem Bewegungsablauf eines Werkzeugschlittens (zb.) in der Produktionstechnik, beide Bewegungsabläufe sind gleich!

Die Differentiation des Bewegungsablaufes in der Produktionstechnik, ergibt damit die Ausgangsbewegung der späteren Animation im Browser, ohne Konstanten, bei einem einfachen Beispiel, vor der Konvertierung!

Die Konvertierungsregel wird bei normalen, konstanten Faktoren durch einen einfachen Koeffizientenvergleich durchgeführt, der nach der Differentiation der Integrale stattfindet. Die sog. Ausgangsbewegung ergibt sich hier bei diesem Beispiel zu:

(f(x)*f'(x)/f''(x))', da F(x), die Animation im Browser sich zu f(x)*f'(x)/f''(x)*s(a,b,c,d)=F(x) ergibt!!!!!

http://www.wichmann.dashosting.de/mathematische%20Basteleien/Integration.html

, siehe ganz oben

Bei einem Beispiel, wie diesem:

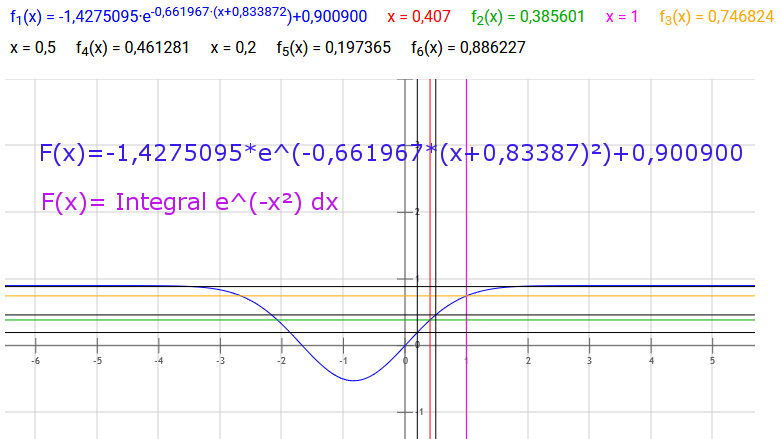
Text erkannt:

\( \begin{array}{l}f_{1}(x)=-1,4275095 \cdot e^{-0,661967 \cdot(x+0,833872)+0,900900} \quad x=0,407 \quad f_{2}(x)=0,385601 \quad x=1 \quad f_{3}(x)=0,746824 \\ x=0,5 \quad f_{4}(x)=0,461281 \quad x=0,2 \quad f_{5}(x)=0,197365 \quad f_{6}(x)=0,886227\end{array} \)

müssten die entsprechnenden Konvertierungsregeln noch ausgearbeitet werden......, fakt wird jedoch auch eine Differentiation des Integrales sein, für die Mathematik! Und bei diesem Beispiel habe ich mir bisher die "Zähne" ausgebissen.

Damit könnte man doch die komplette Integralrechnung durch eine mathematische Konvertierung ersetzen, oder?

Ich weiß selber, dies klingt alles sehr hypothetisch. Viele Grüße!

Comments

Dein Interesse für Mathematik in allen Ehren, aber die Idee, eine neue Art der Integration zu erfinden, funktioniert nicht.

Deine ‚Basteleien‘ wie Du sie selber oben auf der Webseite nennst stimmen nicht, wie schon der dort abgebildete Graph ja auch eindeutig zeigt.

In Deinem Beispiel ist F(x) ein Polynom 5. Grades, der Ausdruck \( \frac{f(x)f‘(x)}{f‘‘(x)} \) eine gebrochen rationale Funktion. Diese Funktionen können nie gleich sein und sind es auch hier nicht.

Die Graphen überlagern sich auch nicht wirklich, sie berühren sich in einem Punkt, das ist alles, man muß nur reinzoomen.

---

Für mich geht das alles nur noch als Spam durch, denn mehr ist das nicht. Nichts wird vernünftig erläutert oder erklärt. Es werden Begriffe und Bezeichnungen herumgeworfen und parallel dazu soll die Anwendung anhand irgendeiner Animation durchgeführt werden, wobei dann noch auf die eigene Homepage verwiesen wird (versteckte Werbung).

 \( \frac{f(x)f‘(x)}{f‘‘(x)} \)

Nutze bitte das richtige Zeichen ' statt ‘ oder verwende f^\prime: \(f^\prime\).

---

Sie haben die Konstanten bei diesem Beispiel vergessen, die sich aus einem Koeffizientenvergleich, nach der Differentiation, ergeben,s(a,b,c,d)! Der erste und der fünfte Graph überlagern sich!

Text erkannt:

\( \begin{array}{l}f_{1}(x)=4 / 5 x^{\wedge} 5-4 / 3 x^{\wedge} 3+x \quad f_{2}(x)=\left(8 x^{\wedge} 7-12 \cdot x^{\wedge} 5+6 x^{\wedge} 3-x\right) /\left(6 x^{\wedge} 2-1\right) \quad \text { Zoom: } x(-2.2) y(-2.2) \quad x=0,408 \quad f_{3}(x)=0,377 \\ f_{4}(x)=0,377 \quad f_{5}(x)=\left(24 / 5 \cdot x^{\wedge} 7-132 / 15 x^{\wedge} 5+22 / 3 x^{\wedge} 3-x\right) /\left(6 x^{\wedge} 2-1\right)\end{array} \)

Integrale werden in der Informatik hauptsächlich numerisch berechnet, da Computer stetige Funktionen nicht exakt "integrieren" können.

---

Also dann etwas ausführlicher:

Die Funktion

 \( f(x)=4x^{4}-4x^{2}+1 \)

ist ein Polynom (ganz-rationale Funktion) vom Grad 4,

Die Stammfunktion \( F(x)=\frac{4}{5} x^{5}-\frac{4}{3} x^{3}+x+c \)

somit ein Polynom 5. Grades, während
\( g(x)=\frac{\frac{24}{5} x^{7}-\frac{132}{15} x^{5}+\frac{22}{3} x^{3}-x}{6 x^{2}-1} \)

eine gebrochen rationale Funktion ist.

Die Funktionen F(x) und g(x) können daher nicht gleich sein, g(x) ist für die Nullstellen des Nenners nicht definiert (auch wenn man hier stetig ergänzen kann).

Ihr Trick funktioniert nur zufällig. Die Erklärung ist, das in diesem speziellen Fall der Grad der Polynome f(x)f‘(x) gleich dem Grad von F(x)f‘‘(x) ist, beides Polynome vom Grad 7.

Nun führen sie noch beliebige Koeffizienten ein, machen ein Koeffizientenvergleich und Voilà, linke Seite = rechte Seite, was jetzt natürlich zu erwarten war (die Komplikationen durch den Bruch wurden dabei geflissentlich übergangen).

Probieren Sie es doch mal mit anderen, einfachen Funktionen aus, wie z.B. f(x) = 4x-4 oder f(x)= \( \frac{1}{x} \).

Sie werden sehen, dass Ihre Methode nicht funktioniert.

Nebenbei: für den Koeffizientenvergleich müssen Sie ohnehin F(x) bereits kennen. Da beißt sich die Katze in den Schwanz.

---

mein Koeffizientenvergleich:

https://de.numberempire.com/equationsolver.php

F(x)=4/5x^5-4/3x^3+x=(a*8x^7-b*12x^5+c*6x^3-d*x)/(6x^2-1)

s(a,b,c,d)*((f(x)*f'(x)/f''(x))'=f(x)

(240*a*x^8+(-216*b-56*a)*x^6+(36*c+60*b)*x^4+(6*d-18*c)*x^2+d)/(6*x^2-1)^2=4*x^4-4*x^2+1

für "a" zb.:

a = (144*x^8+(216*b-192)*x^6+((-36*c)-60*b+88)*x^4+((-6*d)+18*c-16)*x^2-d+1)/(240*x^8-56*x^6)

für "b" zb.:

b = ((240*a-144)*x^8+(192-56*a)*x^6+(36*c-88)*x^4+(6*d-18*c+16)*x^2+d-1)/(216*x^6-60*x^4)

usw.

Ergebnisse des Koeffizientenvergleichs:

a=(144x^8)/(240x^8)=12/20

b=(192-56a)x^6/(216x^6)=132/180

c=-(60b-88)x^4/(36x^4)=22/18

d=1

für die Nullstellen des Nenners des 5. Graphen ist die Funktion nicht definiert, das gebe ich zu, aber die kennt man ja damit....

---

Durch Wiederholung wird es nicht besser.

Ich warte auf Deine Lösung für f(x) = 4x-4 oder f(x) = \( \frac{1}{x} \)

---

f(x) muß mindestens ein Polynom 2. Grades sein.....

---

Wenn man die ganzen Nebelkerzen in Deiner Rechnung beseitigt, machst Du nur Folgendes:

Gegeben ist die Funktion \( f(x)=4x^{4}-4x^{2}+1 \).

Die Stammfunktion F(x) ist gesucht, diese ist ein Polynom 5. Grades, hat also die Form

 \( F(x)=ax^{5}+bx^{4}+cx^{3}+dx^{2}+ex+f \).

Nun wird F(x) abgeleitet und gleich f(x) gesetzt, damit folgt:

\( 4x^{4}-4x^{2}+1 \) = \( 5ax^{4}+4bx^{3}+3cx^{2}+2dx+e\).

Nun vergleichen ergibt d=b=0, e=1, c = -4/3, a=4/5, f beliebig.

Du hast nur benutzt, dass man ein Polynom 5. Grades durch ein Polynom 5. Grades darstellen kann, etwas Selbstverständliches. Das hat nichts mit einer neuen Art der Integration zu tun.

---

Es wäre doch lohnend bei einer Funktion f(x)=e^(-x^2) mit einem entsprechenden F(x) einem Koeffizientenvergleich nachzugehen, habe dies versucht, erhalte da für die konstanten Faktoren jedoch leider einmal ein Polynom und damit stimmt die Ableitung dann nicht mehr. Es wird einen mehrstufigen Koeffizientenvergleich für diese Funktion geben, da bin ich mir sicher. Dies würde bedeuten, daß diese Funktion multipliziert mit einem beliebigen Polynom das Integral der Funktion ergibt. Das F(x)=∫e^(-x^2) existiert, habe ich bei dem weiter oben stehenden Bild gezeigt.

Die Ableitung mit dem normalen Koeffizientenvergleich ergab:

 \(y'={{\left(256\,x^{16}+512\,x^{14}+256\,x^{12}+128\,x^{10}- 160\,x^8-352\,x^6-16\,x^4-24\,x^2+9\right)\,e^ {- x^2 }}\over{256\,x ^{16}+512\,x^{14}+256\,x^{12}-128\,x^{10}-32\,x^8+96\,x^6+16\,x^4-24 \,x^2+9}} \)

y' soll gleich f(x) sein!!!

der Koeffizientenvergleich war nicht korrekt......, er muß mehrstufig sein

---

Sorry, das ist Unsinn und funktioniert nicht. Du verrennst Dich…

Überzeuge Dich an der einfachen Funktion f(x) = 1/x , gerne mit mehrstufigem Koeffizientenvergleich ;-)

---

Lass bitte einfach die Finger von der Mathematik oder verschone uns zumindest damit.

https://www.wolframalpha.com/input?i=integral+e%5E%28-x%5E2%29

Die Methode mit dem Koeffizientenvergleich funktioniert prinzipiell schon und kann man bei Funktionen der Form \(f(x)=p(x)\mathrm{e}^{ax+b}\) verwenden, wobei \(p(x)\) eine ganzrationale Funktion ist. Für die Stammfunktion kann man dann einen Ansatz \(F(x)=q(x)\mathrm{e}^{ax+b}\) machen, wobei \(q(x)\) einen um eins größeren Grad als \(p(x)\) besitzt.

Da braucht man auch nichts mehrstufiges... Was auch immer das im Zusammenhang mit einem Koeffizientenvergleich sein soll.