Aufgabe:
Eigenmann: Wie groß ist der Winkel α?
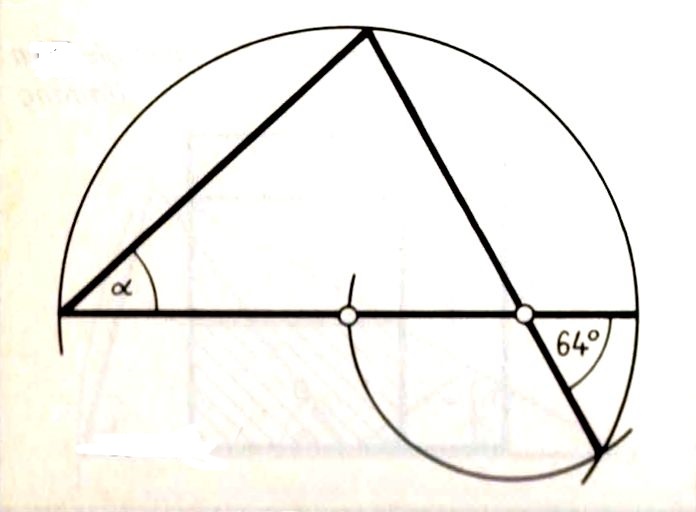
Ohne Taschenrechner; die Figuren sind nicht maßgetreu.
Paul Eigenmann, Aufgabe 1.1.15, ISBN 3-12-722310-2, 1981, S. 5
Problem/Ansatz:
Wer kann helfen? Ich verstehe nicht den Zweck des Schnittes zweier Kreise unten rechts, der aber vermutlich für die Lösung gebraucht wird.