Quadratische Gleichungen: a) 0,2x^2+x+1,4=0 b) 4x+20x+25=0

Question

Ich soll die Gleichung auflösen wenn möglich und dazu eine Zeichnung. Danach soll ich die Lösungsmenge bestimmen:

a) 0,2x^2+x+1,4=0

b) 4x+20x+25=0

 

Kann man danach eine so eine Probe machen um zu gucken ob man das richtig gemcht hat.

Comments

Hast du bei der zweiten Aufgabe kein Quadrat?

---

nein  glaub nicht ...:S

---

das ist wahrscheilich falsch.. weil es irgenm.wie anders ist also die Beispielaufgabe... schade :(

Answer 1

a) 0,2x^2+x+1,4=0         |*5

x^2 + 5x + 7 = 0

x_1,2 = 0.5 (-5 ±√(25 - 28))

Hat keine reelle Lösung.

Kontrolle y=0,2x^2+x+1,4 aufzeichnen und sehen, dass die Kurve die x-Achse nicht schneidet:

 

b) 4x+20x+25=0 Das ist gar keine quadratische Gleichung.

Ich nehme mal 4x^2 + 20x + 25 = 0

Der Graph zu y = 4x^2 + 20x + 25 sieht so aus:

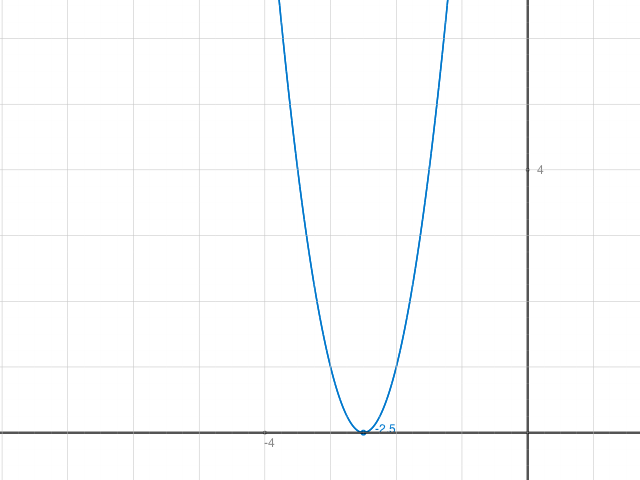
Somit sollte man den Punkt der Parabel auf der x-Achse berechnen können:

4x^2 + 20x + 25 = 0     |:4

x^2 + 5x + 6.25 = 0             | Hier erkennt man einen Binom

x^2 + 2"2.5x + 2.5^2 = 0

(x + 2.5)^2 = 0           |Wurzel draus

x + 2.5 = ±0 = 0

x = -2.5

Kontrolle: Graph.

Oder -2.5 in 4x^2 + 20x + 25 = 0 einsetzen:

4*(-2.5)^2 + 20*(-2.5) + 25 = 0

4*6.25 - 50 + 25 =0 ok.