Nach Funktionsuntersuchung auf Dmath U(t)= 2*e^ (-(t-3)²) die Umsätze beschreiben?

Question

U(t)= 2*e^-(t-3)²
- Funktionsuntersuchung auf Dmath
- Beschreibung der Umsätze in Abhängigkeit von der Zeit
- Das betreffende Produkt wird vom Markt genommen, wenn der Umsatz unter 0,1 ME sinkt. Wann geschieht dies?
Antwort 1 Funktionsuntersuchung durchführen ist klar
Frage 2 Was muss hier angewendet werden?
Frage 3 U(t) = 0,1 setzen
so weit sind wir hier gekommen:
e^{-(t-3)²}=0,1/2   
wie geht es dann weiter?
ist für ein Vortrag in Mathe

Answer 1

Frage 3 U(t) = 0,1 setzen
so weit sind wir hier gekommen:
e^-(t-3)² = 0,1/2 = 0.05 = 1/20 = 20^{-1}   |Kehrwert

e^(t-3)² = 20                  | ln links und rechts

(t-3)^2 = ln (20)                | √

t - 3 = ± √( ln (20))

t = 3 ±√(ln (20))

gibt mathematisch 2 Resultate für t.

Berechnet beide und vergleicht mit eurer Kurve und den Voraussetzungen. Das Resultat kleiner als 3 ist nicht erwünscht. So sieht eure Umsatzkurve aus: 

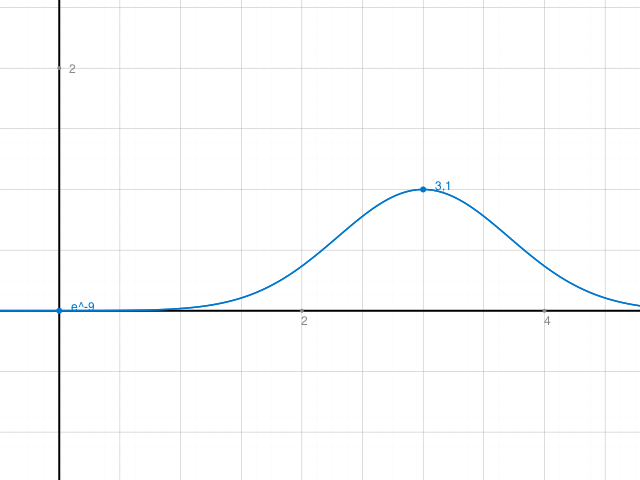
Frage 2. Beschreiben heisst hier wohl, dass ihr ein paar Sätze schreibt. Hier eine Kurzversion, die ihr mit auren Zahlen… ausbauen solltet.

Zu Beginn muss man bis t=1 (oder was euch da gefällt) warten, bis man etwas verkauft. Dann wächst die Umsatzzunahme bis zur Wendestelle. Nach der Wendestelle nimmt der Umsatz immer weniger zu bist er zum Zeitpunkt t= 3 stagniert und dann gleich zurückgeht, wie er angestiegen ist.