Aufgabe:
Untersuchung ganzrationaler Funktionen:
Gegeben ist die Funktion f mit der Gleichung:
$$ f(x)=\frac{1}{6} \cdot x^{3}-x^{2}+4 $$
Die Abbildung 1 zeigt den Graphen der Funktion \( f \).
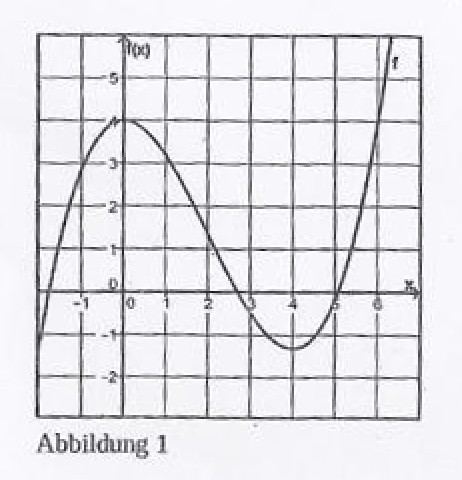
a) (1) Ermittein Sie rechnerisch die Koordinaten des lokalen Hochpunktes und die Koordinaten des lokalen Tiefpunktes des Graphen der Funktion \( f \).
(2) Berechnen Sie die Steigung der Geraden durch die beiden in a) (1) ermittelten lokalen Extrempumkte.
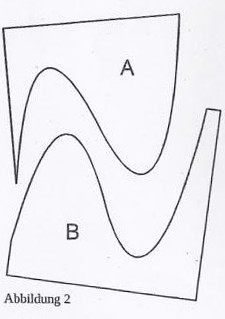
b) Die Abbildung 2 zeigt, wie durch den Graphen der Funktion \( f \) der in Abbildung 1 dargestellte Bereich des Koordinatensystems in zwei Teile A und B geteilt wird. Entscheiden Sie begründet, ob der Punkt \( P(2 \mid 1,3) \) zu A oder zu B gehört.