Erst dachte ich: nur eine primitive Iteration wie im Bild:
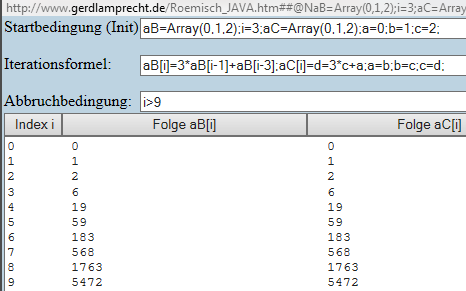
ABER dann fand ich, dass diese Zahlenfolge identisch ist zu
A052541(n) - A051541(n-1)
mit der expliziten Formel A052541(n) = 3^n*hyg3F2(1/3-n/3,2/3-n/3,-n/3,1/2-n/2,-n/2,-1/4)
kann jeder beliebige reelle Wert berechnet werden
siehe Umkehrfunktionen Rechner mit hypergeometrischen Funktionen http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php
A052541(1/2)= 1.8169008062911036734412566...
Man könnte sogar den stufenlosen Funktionsverlauf zeichnen...