Die Frage ist so nicht beantwortbar. vgl Kommentar
Ich ändere sie deshalb so, wie man daraus etwas Vernünftiges machen kann.
f(x+a)-f(x-a) =
2a
| f(x)=kx+d einsetzen
= k(x+a) + d - (k(x-a) +d)
2a
= kx+ka + d - (kx -ka +d)
2a
= ka + ka
2a
= 2ka |kürzen
2a
= k
Interpretation: Die mittlere Steigung von f(x) zwischen den Stellen (x-a) und (x+a) ist k.
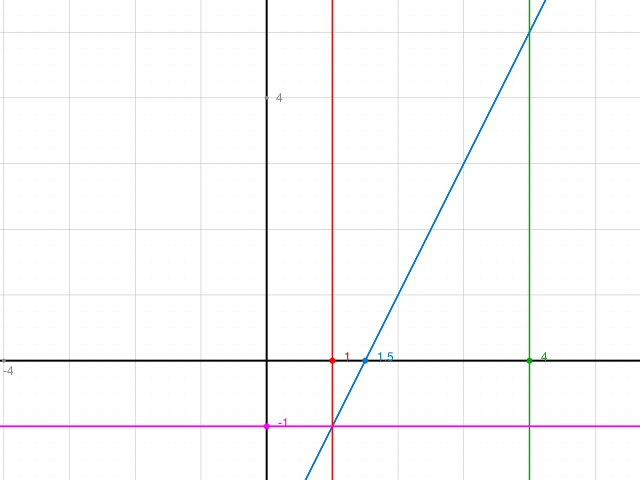
Skizze für k=2, d= -3, x=2.5, a = 1.5 zeigt das am Steigungsdreieck (violett, grün, blau) zwischen x-a = 1 und x+a = 2.
Horizontal hat man dort 2a = 3.
Vertikal f(4) - f(1) = 6
und 6/3 = 2 wie gewünscht.