Um die Wendepunkte der Funktion
f(x) = -x4/4 + x3
zu finden, musst Du die zweite Ableitung 0 setzen, also
f'(x) = -x3 + 3x2
f''(x) = -3x2 + 6x
0 setzen:
6x = 3x2
x * 6 = x * (3x)
x1 = 0
x2 = 2
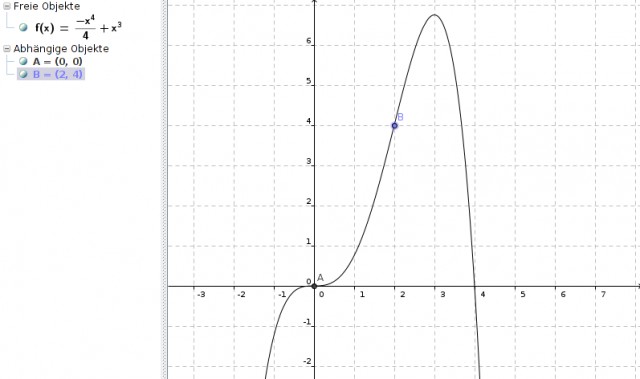 Die Wendestellen sind also x1 = 0 und x2 = 2.
Die Wendestellen sind also x1 = 0 und x2 = 2.
Um die entsprechenden y-Koordinaten zu erhalten, musst Du die Wendestellen in die Ursprungsfunktion einsetzen:
f(0) = -04/4 + 03 = 0
f(2) = -24/4 + 23 = -4 + 8 = 4
Damit lauten die Wendepunkte
(0|0) und (2|4)