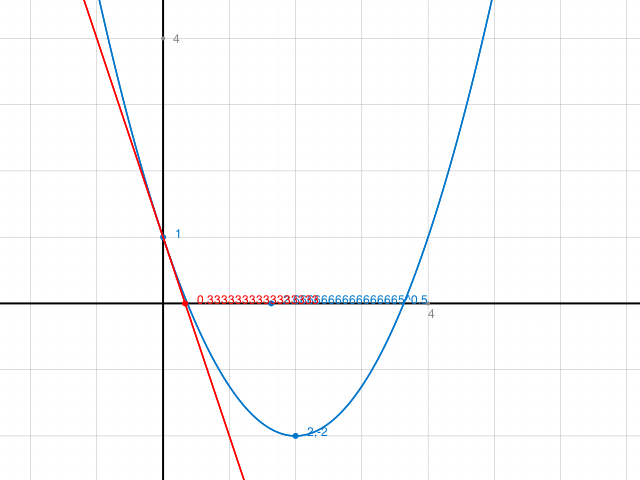
Der Grapf einer Polynomfunktion f vom Grad 2 besitzt den Tiefpunkt T(2/-2).
Die Steigung der Tangente an der Stelle 0 beträgt -3.
Benutze hier unbedingt die altbekannte Scheitelpunktform der Parabelgleichung, So sparst du dir einen Teil der Rechnung.
T(2/-2) ist Scheitelpunkt. Die Öffnung a muss via die Steigung bestimmt werden.
Ansatz
y = a (x - 2)^2 - 2
y = a (x^2 - 4x + 4) - 2 = a x^2 - 4ax + 4a - 2
y ' = 2ax - 4a
f ' (0) = - 4a = - 3
a = 3/4
Funktionsgleichung: y = 3/4 (x - 2)^2 - 2