Flächeninhalt eines Rechtecks möglicht groß optimieren, wie?

Question

Ich habe ein gleichschenkliges Dreieck mit der Höhe und der Grundseite gegeben.

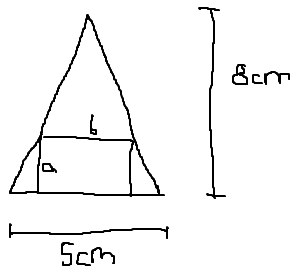
Nun soll ich die Seiten a und b so wählen, dass der Flächeninhalt des Recheckes (welches im Dreieck liegt), möglichst groß wird.

Mit einem Gleichseitigen Dreieck ist das auch kein Problem aber mit einem Gleichschenkligen habe ich meine Schwierigkeiten.

Ziel ist ja eine quadratische Funktion (Parabel), wobei dann der Scheitelpunkt mein gewünschtes Ergebnis ist. Ich bräuchte den richtigen Ansatz.

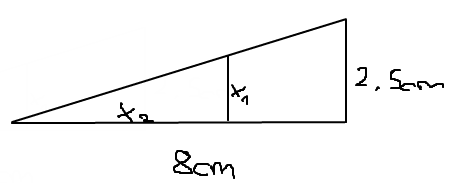
Ich bin jetzt darauf gekommen, es mit dem Strahlensatz zu probieren, aber habe jetzt 2 Unbekannte, wie gehe ich nun weiter vor?

Answer 1

x1 : x2 = 2.5 : 8

x1 = 2.5x2 : 8

wegen x2 = (8-a)     und x1 = b/2

b/2 = 2.5(8-a) / 8          |*2

b = 5(8-a) / 8

Fläche(a) = a*b = 5(8-a)a / 8        

Das wäre die gewünschte Parabelgleichung einer nach unten geöffneten Parabel. Nullstellen bei a1= 8 und a2=0. Scheitelpunkt in der Mitte. Also bei a = 4 cm

Zugehöriges b = 5*4/8 = 2.5 cm

Maximale Fläche 2.5*4=10 cm^2

Man muss also nicht unbedingt die Scheitelpunktform erstellen. Verboten ist das aber nicht.

Comments

x2 ist doch 8-a und x1 ist b/2?

---

Stimmt! ich habe a und b umbenannt. In der Skizze sind die anders.

Inzwischen sollte es zurückgetauscht sein.

---

Vielen dank erstmal, aber wie kommst du ohne die quadratische Ergänzung darauf, dass der Scheitel 4 ist?

---

Parabeln 2. Grades sind Symmetrisch. Wenn du 2 Nullstellen hast, einfach in der Mitte.