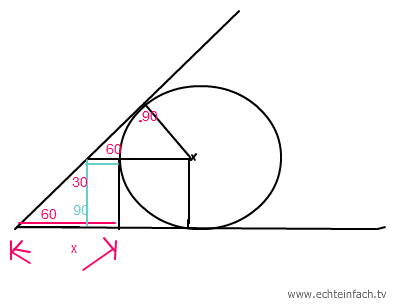
in einem gleichseitigen dreieck sind alle Winkel 60° und nun geht es darum die Grundseite a zu bestimmen,
a = 4*(2*r) +2x
um x zu bestimmen muss man mit sin und tan arbeiten
einmal x=( r/sin 60°) +tan 60° *r
also ist dann
a=4*(2r)+2*(r/sin0°)+tan 60° *r
=r*(8+2/sin°+2*tan60°) =2r(4+ 1/sin 60° +tan 60°)
die Fläche des Dreieckes ist
A=(a²*√3)/4 nun a einsetzen
A=((2r*(4+1/sin 60°+tan 60°))² *√3)/4