In einem rechtwinkligen Dreieck sind von den Größe b und h gegeben, Berechnen Sie a, c, p, q, α und β.
Planfigur:
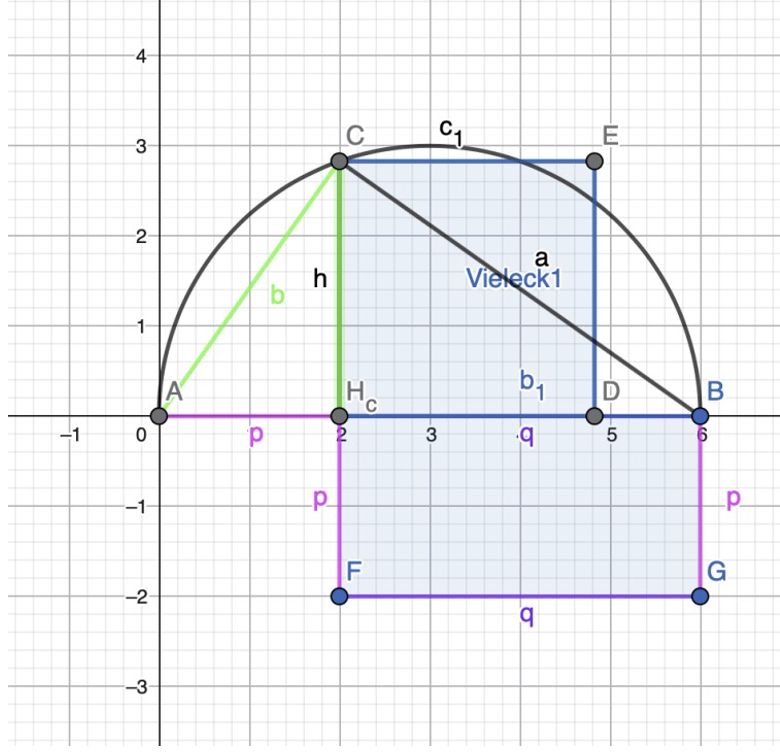
Nach dem Höhensatz des Euklidischen gilt : \( h^2=p q \) , wo bei \( p+q=c\)
Nach dem Satz des Pythagoras:
\( b^2=h^2+p^2 \) →. \(p^2=b^2-h^2 \) → \(p=\sqrt{b^2-h^2 }\)
Berechnung Winkel \(α\) :
\( \ sin(α)=\frac{h}{b}\)
\(α= \sin^{-1} (\frac{h}{b}) \)
Berechnung Winkel \(β\) :
\( β=90°-α \)
Berechnung \(a\) :
\( \sin (90°-α)=\frac{h}{a} \) → \(a=\frac{h}{\sin (90°-α)} \)
Berechnung \(c\) mit Pythagoras:
\(c= \sqrt{a^2+b^2} \)
Berechnung \(q\) :
\(q=c-p=c-\sqrt{b^2-h^2 }\)