Anteil der schraffierten Fläche in Prozent bestimmen.

Question

Bestimme den Anteil der schraffierten Fläche an der gesamten Rechtecksfläche:

Comments

Ich vermute, dass wenn du die Strecken ausmißt, die von mir angenomme Symmetrie feststellen wirst. Selbst die Schraffur stimmt bis aufs Haar überein. Ansonsten frag doch vorab einmal deinen Lehrer. Dies ist wahrscheinlich das einfachste. Zeig ihm die von dir eingetragenen Maße und frag ob du Symmetrie annehmen kannst.

Answer 1

u + 2u = b/2 -----> u = b/6

Und nun kommst du selbst weiter.

Comments

Warum machst du dieselbe unbegründete Annahme wie Marvin und Georg ?

---

Weil die Fragestellung so aussieht, als würde b halbiert.

Da das eine Schulaufgabe ist, gehe ich mal davon aus, dass der Lehrer das so gemeint hatte.

---

Da würde ich auch mal von ausgehen. Denn im Grunde müsste die mittlere Trennung nicht mal senkrecht zu den Kanten sein. Das würde man hier aber sicher auch voraussetzen.

---

weil die Fragestellung so aussieht, als würde b halbiert

Das ist eine ziemlich schwache Begründung. Es sieht auch so aus, als wären alle Dreiecke rechtwinklig. (Was für ein Rechteck im DIN-A - Format tatsächlich zutreffen würde und für die Beantwortung der Frage völlig unerheblich ist.)

Da das eine Schulaufgabe ist, gehe ich mal davon aus, dass der Lehrer das so gemeint hatte.

Es ist aber eine Präsentation. Vielleicht wird da etwas mehr verlangt.

---

Soweit ich deine Argumentation überflogen habe stimmt sie mit meiner überein. Ja Man kann die Strahlensätze als Beweis anführen oder es noch ein bißchen komplizierter herleiten. Das Ergebnis bleibt bei mir immer dasselbe.

Würde bei deiner Herleitung auch mein Ergebnis herauskommen?

---

Ja. Ich hoffe, dass der Fragesteller dann auch auf 5ab/12 kommt.

Wenn er will und Strahlensätze genug gut kennt, kann er ja auch noch b im Verhältnis 2: 1 oder 3:1 unterteilen. vielleicht lässt sich da noch was verallgemeinern.

---

Dankeschön! :) ich muss aber auch beweisen, wieso das b/2 sind, weil das in der Aufgabenstellung nicht steht

---

Das kannst du nicht beweisen, wenn du oben im Bild die ganze Aufgabenstellung angegeben hast. Genauso wenig kannst du beweisen, dass die Linie, die bei mir zwei mal mit a/2 beschriftet ist, senkrecht auf b steht.

Darum kannst du ja auch noch ein paar weitere Fälle durchrechnen, wie ich dir oben vorgeschlagen habe.

---

Wenn die mittlere senkrechte Linie das Rechteck halbiert ist alles weitere lückenlos beweisbar. Führe ich dann gerne auf Wunsch vor.

---

Habe ich ja bewiesen. Aber du kannst es gern nochmals ausführlicher machen.

Answer 2

In der Schule?Wäre gut zu wissen zu wechem Thema du das machen musst. Schau dir das Rechteck im Gesamten an. Dort hast du 2 Seitenflächen a(Höhe) und b(Länge) gegeben. Das Rechteck wird in der Mitte in zwei gleich große Rechtecke geteilt.

Betrachte z.b. die rechte Hälfe. Die weiße Fläche unten links in der rechten Hälfte bildet mit der schraffierten Fläche oben links in der rechten Hälfte ein rechtwinkliges Dreieck. Die beiden Seiten am rechten Winkel sind nun a und b/2.

Damit kannst du den Winkel dieses Dreiecks unten links in der rechten Hälfte ausrechnen. Hieraus folgt auch der Winkel dieses Dreiecks oben links in der rechten Hälfte. 

Was kannst du nun über die anliegenden Winkel sagen? Weißt du durch welche Kriterien ein Dreieck eindeutig bestimmt ist? (SWS, WSW ... )

Wo kannst du noch rechtwinklige Dreiecke bilden auf der rechten Hälfte? Welche Winkel kannst du berechnen. Schau dir das alles an.

Mit der Methode kannst du immer mehr Seiten und Winkel der einzelnen Figuren berechnen.

Welche Flächen lassen sich hiermit nun am einfachsten berechnen?

Und was fällt dir auf wenn du dir die linke und die rechte Hälfte anschaust?

Ich hoffe mal das war nicht zu viel auf einmal . Viel Spaß beim rechnen :)

Comments

Das bringt mich schon um einiges weiter!

Was ich jedoch nicht verstehe ist, wie ich mit den Seiten des Dreiecks die Winkel berechnen kann, denn bisher haben wir das mit sinus cosinus und tangens gemacht, aber nicht mit Variablen, sondern konkreten Zahlen..der Taschenrechner kann auch nichts mit Variablen anfangen :/

---

Darum geht es ja in der Aufgabe. Du hast ja keine festen Seitenlängen gegeben. Deswegen machst du doch eine Präsentation. Also um zu zeigen wie man sowas im generellen löst. Ich denke nicht ,dass du die Seiten mit dem Lineal nachmessen sollst.
Du sollst ja, denke ich mal, einen kompletten Lösungsweg schildern und zwar so in der Art wie ich das gemacht habe ,aber natürlich vollständig.

---

Nein ich muss auch wirklich am Ende auf eine Lösung kommen wie z.B. 50% und was ich schildern muss ist, wie ich darauf gekommen bin und die ganzen Rechenschritte, also es darf kein Text auf der Präsentation sein

---

Oh : "Bestimmen sie den ANTEIL..." . Hab ich doch glatt überlesen. Ich schaus mir nochmal an.

---

Okay neuer Versuch. Bis jetzt kann ich dir meine Idee geben. Einen direkten Beweis für alles habe ich noch nicht. Also die kleinen Dreiecke sind beide gleich groß(Beweis kannst dir ja denken).

Die Grundfläche des kleinen beträgt b/2 und die Höhe Beträgt a/6. Das kleine Dreieck passt nun 4 mal in das große Dreieck. Das Ergebnis kann man hiermit berechnen,aber warum genau das so ist kann ich dir im Moment noch nicht sagen.(Ich habe mir die Lösung teilweise zeichnerisch angeschaut).

Vielleicht kann dir ja wer anders auf die Sprünge helfen wie genau man beweistechnisch darauf kommt

---

Deine Idee bringt mich schon ziemlich weiter, ich muss jetzt nur noch beweisen, wieso die Höhe des kleinen Dreiecks a/6 ist und den Rest schaffe ich hoffentlich alleine :)

Answer 3

Bezüglich der mittleren Achse in y-Richtung sind die
Flächeninhalte links und rechts gleich.
Ich betrachte daher jetzt den rechten Teil.
Die linke Seite wird von der Diagonalen halbiert:
Oben und unten bezeichne ich die Seitenlänge mit a.
links mit b/2 und rechts mit b



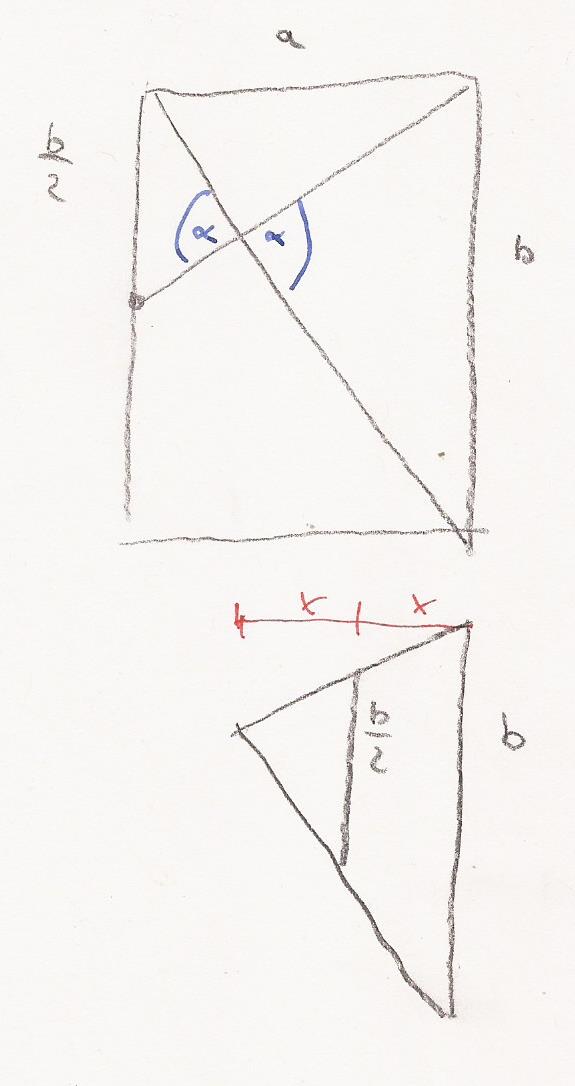
Die schraffierten Dreiecke sind von den Winkeln gleich.
Das linke Dreieck ist kleiner.
Das linke Dreieck füge ich einmal in das rechte Dreieck ein.
Die Grundlinien der Dreiecke sind b und b/2.
Die Höhen der Dreiecke sind x = a/3  und 2*x =
2 * ( a / 3 )

Als Fläche ergibt sich

[ b * ( 2*a/3 )] / 2  plus
[ b/2 * ( a/3) ] / 2

Die Fläche muß dann noch mit der Gesamtfläche a * b
in Beziehung gesetzt werden.

Ich habe heraus : 5*ab / 12

Comments

Bezüglich der mittleren Achse in y-Richtung sind die Flächeninhalte links und rechts gleich.

Wer sagt das ?