Insbesondere ist die Aufgabe so nicht mehr eindeutig gestellt.
Ich nehme einfach mal an, dass die folgende Kanalform (im Querschnitt) gemeint ist:
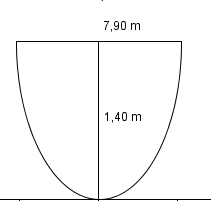
Für die nächste Aufgabe muss nun die obere Fläche im folgenden Bild berechnet werden:

und mit der Länge 1550m malgenommen werden.
(Okay, man muss dazu sagen, dass das Bild nicht den echten Proportionen entspricht.)
Dafür benutzt man am besten die folgende Darstellung der Ellipse:
$$ y = \pm \frac { b } { a } \sqrt { a ^ { 2 } - x ^ { 2 } } $$
mit den Halbachsen a und b, die in diesem Fall
a = 1.4 m
b = 3.95 m
lauten.
Man erhält die folgende Graphik:
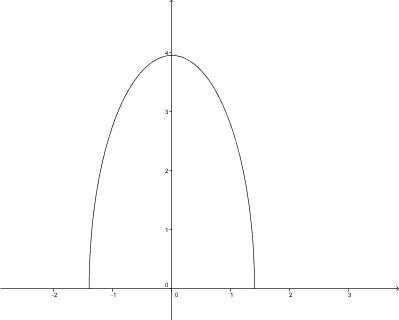
Für die gesuchte Fläche muss nun das Integral von 0 bis 0.42 berechnet und mit zwei malgenommen werden.
Die gesuchte Fläche ist also
$$ \int _ { 0 } ^ { c } \frac { b } { a } \sqrt { a ^ { 2 } - x ^ { 2 } } $$
Die Lösung des Integrals kann zum Beispiel folgendermaßen erfolgen:
$$ \int \sqrt { a ^ { 2 } - x ^ { 2 } } d x $$
Substituiere: \( x = a \sin ( t ) , \quad d x = a \cos ( t ) d t , t = \arcsin \frac { x } { a } \)
$$ = a ^ { 2 } \int \sqrt { 1 - \sin ^ { 2 } t } \cos ( t ) d t = a ^ { 2 } \int \cos ^ { 2 } ( t ) d t = \frac { a ^ { 2 } } { 2 } ( t + \sin ( t ) \cos ( t ) ) $$
$$ = \frac { a ^ { 2 } } { 2 } \left( \arcsin \frac { x } { a } + \frac { x } { a } \cos \arcsin \frac { x } { a } \right) $$
Nun könnte man noch cos(arcsin(a/b)) = sqrt(1-x²/a²) verwenden, aber da ja sowieso Zahlenwerte gegeben sind, muss das nicht unbedingt sein.
Der Ausdruck muss nun noch mit 2b/a malgenommen werden und von 0 bis c ausgewertet werden.
Mit den entsprechenden Zahlenwerten erhält man dann:
A ≈ 3.2675 m2
Damit erhält man für das Volumen:
V ≈ 3.2675 m2 * 1550m = 5064,625 m3 = 5064625 l
Also für die Leistung
5064625l / 720 min = 7034,201 l/min
Nun muss entsprechend für die nächste Aufgabe die Fläche zwischen 0 und 0.9 berechnet werden. Auf dem selben Weg erhält man
A2 = 6.5843 m2
V2 = 10205665 l
t = V2/P ≈ 1450,86 min = 24,1811 h