gegeben ist eine Parabelzeichnung, aus der ich die Funktion 1/8x^2 herausgefunden habe. Der Flächeninhalt beträgt 5,33 FE zwischen -4 und 4. Wie kann ich nun jedoch das Volumen bestimmen? Wäre es das Integral * pi?
Bitte gebt mir keine direkten Antworten! :)
Der Kanal
Der Boden eines 2 km langen Kanals hat die Form einer Parabel. Dabei entspricht eine Längeneinheit in der Realität einem Meter.
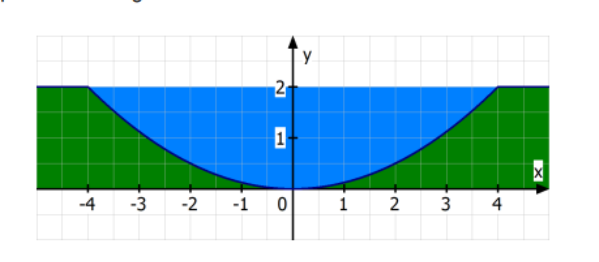
a) Berechnen Sie den Inhalt der Querschnittsfläche eines solchen Kanals. [10,67 m^2]
b) Wie viel Wasser befindet sich im Kanal, wenn er ganz gefüllt ist? [21333 m^3]
c) Wie viel Prozent der maimalen Wassermenge befindet sich im Kanal, wenn er nur bis zur halben Höhe gefüllt ist? [35,36 %]
$$ \begin{array}{l}{\text { Durch Ablesen: } S(0|0) \text { ; P }(-4 / 2) \text { ; } Q(4 | 2)} \\ {\text { S, } \operatorname{in} f(x)} \\ {f(x)=a(x-0)^{2}-0} \\ {f(x)=a\left(x^{2}\right)} \\ \text{P in }f(x) \\ 2= a \cdot\left(4^{2}\right) \\ 2= 16 a \quad |: 16 \\ \frac{1}{8}={a} \\ {f(x)=\frac{1}{8} x^{2}}\end{array} $$