Genau ein gemeinsamer Punkt heisst, dass die Schnittpunktberechnung nur genau eine Lösung hat.
Schnittpunktberechnung: Funktionsgleichungen gleichsetzen.
-x²+3 = x²-4x +q
0 = 2x^2 - 4x + q-3
Das ist eine quadratische Gleichung zur Berechnung von x.
In die Mitternachtsformel müsste a=2, b= -4 und c = (q-3) eingesetzt werden.
Da nun nur eine Lösung gewünscht ist, muss in der Diskriminante unter der Wurzel
b^2 - 4ac = 0 sein.
Also: 16 - 4*2*(q-3) = 0 |:8
2 - (q-3) = 0
5 - q = 0
5 = q
Probe: Skizze mit f(x) = -x²+3 und g(x)= x²- 4x +5
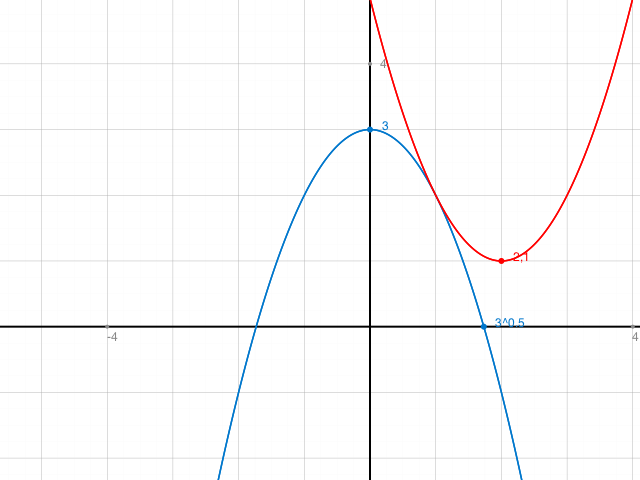
Es gilt übrigens T(1|2). Wir mussten den Punkt aber nicht berechnen, um das q zu bestimmen.