Berechnung und Zeichnung der Graphen von y=f(x)=-x+4 und y=g(x)=2x+1, Schnittpunkt und (3,5|9)

Question

Zwei Funktionen sind durch Gleichungen y=f(x)=-x+4 und y=g(x)=2x+1 gegeben.
Zeichne die beiden Funktionen im Intervall von -2 bis +5 ins Koordinatensystem ein
Die beiden Graphen schneiden im Punkt S. Lies den Schnittpunkt S aus dem Koordinatensystem ab und weise ihn durch Berechnung nach.
Berechne den Abstand des Punktes S vom Koordinatenursprung.
Überprüfe,ob das Zahlenpaar (3,5/9)zur Funktion g(x) gehöhrt und Begründe

Answer 1

Hi,

zur Zeichnung:

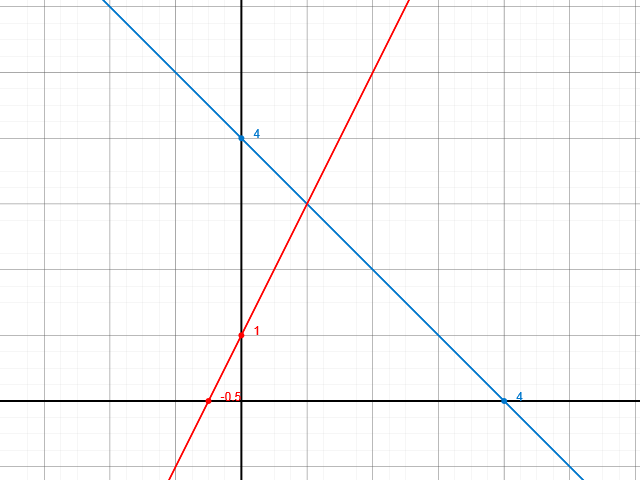
Damit ist der Schnittpunkt bei S(1|3) abzulesen.

 

Kontrolle durch Rechnung, indem man beide Funktionen gleichsetzt:

f(x)=g(x)

-x+4=2x+1        |+x-1

3x=3                  |:3

x=1

 

Nun damit in eine der Funktionsgleichungen (z.B. f(x))

f(1)=-1+4=3

Damit ist auch rechnerisch gezeigt -> S(1|3) passt.

 

 

Abstand zum Ursprung:

Denke Dir ein rechtwinkliges Dreieck.

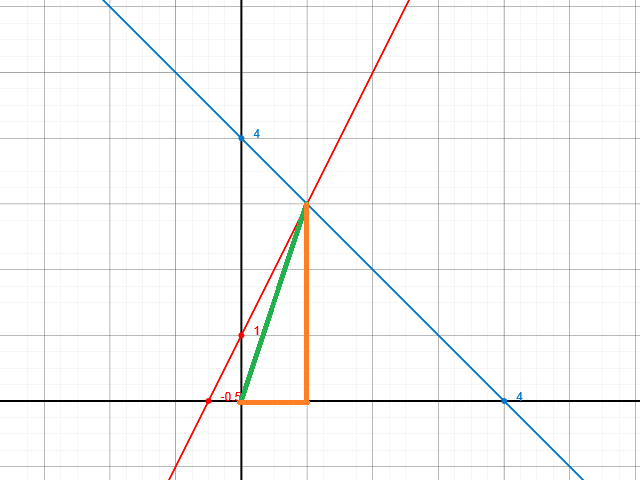
Die grüne Hypotenuse gilt es zu bestimmen. Die orangenen Katheten sind dank des Schnittpunktes bekannt:

x²=1²+3²=10

x=√10

 

Der Abstand zum Ursprung ist also √10 LE   (Längeneinheiten).

 

Punktprobe:

Liegt der Punkt P (3,5|9) auf g(x)?

Setzen wir den x-Wert in g(x) ein ->

g(3,5)=2*3,5+1=7+1=8

-> Der y-Wert ist ein anderer wie verlangt. Also; Nein, der Punkt liegt nicht auf g(x).

 

Verstanden? ;)

Answer 2

a.) Die Zeichnung kannst du zum Beispiel erstellen, indem du jeweils zwei Punkte durch das Einsetzen von x-Werten berechnest und diese Punkte miteinander geradlinig verbindest.

b.) Für den Schnittpunkt gilt

f(x) = g(x)
-x+4 = 2x + 1 |+x
4 = 3x + 1 |-1
3 = 3x  |:3

x = 1

Also P(1, 3).

Das deckt sich mit dem Schnittpunkt, der sich aus der Grafik ablesen lässt.

c.) Den Abstand erhält man mit dem Satz des Pythagoras:

d² = 1² + 3² = 10

d = √10

d.) Hierfür setzt man den Punkt in die Funktion ein und prüft, ob sich eine wahre Aussage ergibt:

9 = 2*3.5 + 1

9 = 7+1

9 = 8

Das ist offensichtlich falsch. Also gehört der Punkt nicht zum Schaubild von g.