Extrema
f(x) = (e
x - k)
2f ´ ( x ) = 2 * ( e^x - k ) * e^x
2 * ( e^x - k ) * e^x = 0
Ein Produkt ist dann 0 wenn mindestens einer der Faktoren 0 ist. Also
e^x - k = 0
dasselbe wie oben
( ln ( k ) | 0 ) für k > 0
ansonsten keinen Extrempunkt
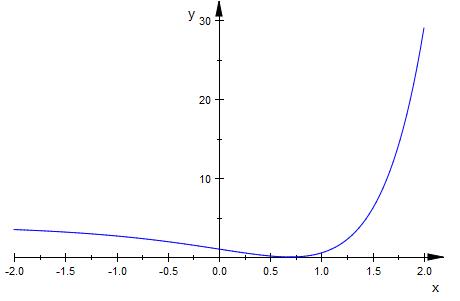
Hier der Graph für k = 2