Vorbemerkung : hier im Forum wird üblicherweise das " du " verwendet.
Dankeschön! Konnte es gut nachvollziehen.
Die allgemeine Form für den Scheitelpunkt ist dann ax2 +b richtig?
Wenn du von der Normalform der Parabel
f ( x ) = a*x^2 + b*x + c
ausgehst, dann ist der x-Wert des Scheitelpunkts
f ´( x ) = 2*a*x + b
bei
2*a*x + b = 0
Vorbemerkung : wenn du eine 2.Frage stellen willst, dann stelle diese als
neue Frage ein. Damit vergrößerst du den Kreis möglicher Antwortgeber.
In der nächsten Aufgabe soll ich einen Funktionsterm für die Parabelschar angeben. Es ist eine Skizze gegeben auf der mehrere Parabeln abgebildet sind, die alle einen unterschiedlichen Scheitel haben. eine bei (-1/-2) dann (0/0) dann 1/2) dann (2/4).
Der Term soll beliebig sein , jedoch soll ich im Nachhinein begründen ob es eine Schar von Parabeln zweiter Ordnung gibt, sodass die Scheitel auf der Kurve K mit (2/x) liegen.
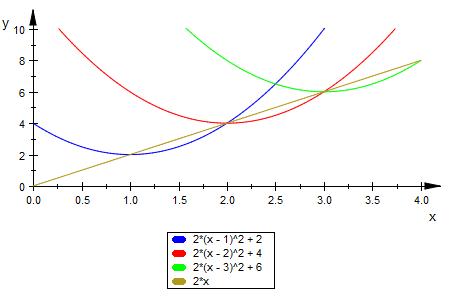
Die Scheitelpunkte liegen alle auf den Punkten ( xs | 2 * xs ).
( jedenfalls wenn ich die angegebenen Punkte richtig deute )
ich benutze wieder die Scheitelpunktform
y = x^2 ( Normalparabel )
y = a * x^2 ( flachere oder steilere Parabel )
y = a * ( x - b)^2 ( zusätzlich nach rechts oder links verschobene Parabel )
y = a * ( x - b)^2 + c ( zusätzlich noch nach oben oder unten verschoben )
Scheitelpunkt ( b | c )
Für den Scheitelpunkt gilt auch ( xs | 2 * xs ).
Also
Scheitelpunkt ( b | 2 * b )
Die Funktionsschar ist die Funktion
f ( x ) = a * ( x - b )^2 + 2 * b
Beispiel
a = 1